(2x²-3x-2):(x-2)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
TT
26 tháng 10 2020
Nếu nhớ không nhầm thì hướng dẫn chi tiết cho rồi :vv
\(x^7+x^2+1=x\left(x^6-1\right)+\left(x^2+x+1\right)\)
\(=x\left(x^3-1\right)\left(x^3+1\right)+\left(x^2+x+1\right)\)
\(=x\left(x-1\right)\left(x+1\right)\left(x^2-x+1\right)\left(x^2+x+1\right)+\left(x^2+x+1\right)\)
\(=\left(x^2+x+1\right)\left[\left(x^3-x\right)\left(x^2-x+1\right)+1\right]\)
P/s : ko chắc lém :)))
4 tháng 11 2016
a)\(\frac{\left(x+2\right)P}{x-2}=\frac{\left(x+2\right)^2P}{\left(x-2\right)\left(x+2\right)}=\frac{\left(x+2\right)^2P}{x^2-4}=\frac{\left(x-1\right)Q}{x^2-4}\Rightarrow\left(x+2\right)^2P=\left(x-1\right)Q\)
\(\Rightarrow\frac{P}{Q}=\frac{x-1}{\left(x+2\right)^2}\)
b) Từ gt,ta có :\(\left(x+2\right)\left(x^2-2x+1\right)P=\left(x^2-1\right)\left(x-2\right)Q\)
\(\Leftrightarrow\left(x+2\right)\left(x-1\right)^2P=\left(x-1\right)\left(x+1\right)\left(x-2\right)Q\)
\(\Leftrightarrow\left(x+2\right)\left(x-1\right)P=\left(x+1\right)\left(x-2\right)Q\)
\(\Rightarrow\frac{P}{Q}=\frac{\left(x+1\right)\left(x-2\right)}{\left(x+2\right)\left(x-1\right)}=\frac{x^2-x-2}{x^2+x-2}\)
Ở đây có nhiều cặp đa thức (P ; Q) thỏa mãn lắm ! Mình xét P/Q để chỉ rằng chúng tỉ lệ với 2 đa thức ở vế phải
Ví dụ : Câu a : P = 2 - 2x thì Q = -2x2 - 8x - 8
28 tháng 7 2021
\(\left(25-m^2\right)=\left(5-m\right)\left(5+m\right)\)
G
10 tháng 8 2023
\(4a^2b^2-\left(a^2+b^2-c^2\right)^2\)
\(=4a^2b^2-2ab\left(a^2+b^2-c^2\right)+2ab\left(a^2+b^2-c^2\right)-\left(a^2+b^2-c^2\right)^2\)
\(=2ab\left[2ab-\left(a^2+b^2-c^2\right)\right]+\left(a^2+b^2-c^2\right)\left[2ab-\left(a^2+b^2-c^2\right)\right]\)
\(=\left(2ab+a^2+b^2-c^2\right)\left(2ab-a^2-b^2+c^2\right)\)
\(=\left(a^2+ab+ab+b^2-c^2\right)\left[c^2-\left(a^2-ab-ab+b^2\right)\right]\)
\(=\left[a\left(a+b\right)+b\left(a+b\right)-c^2\right]\left[c^2-\left(a\left(a-b\right)-b\left(a-b\right)\right)\right]\)
\(=\left[\left(a+b\right)^2-c^2\right]\left[c^2-\left(a-b\right)^2\right]\)
\(=\left[\left(a+b\right)^2-c\left(a+b\right)+c\left(a+b\right)-c^2\right]\left[c^2+c\left(a-b\right)-c\left(a-b\right)-\left(a-b\right)^2\right]\)
\(=\left[\left(a+b\right)\left(a+b-c\right)+c\left(a+b-c\right)\right]\left[c\left(c+a-b\right)-\left(a-b\right)\left(c+a-b\right)\right]\)
\(=\left(a+b+c\right)\left(a+b-c\right)\left(c+a-b\right)\left(c-a+b\right)\)
28 tháng 7 2021
\(10a-25-a^2=-\left(a^2-10a+25\right)=-\left(a^2-2.a.5+5^2\right)=-\left(a-5\right)^2\)
28 tháng 7 2021
a,\(8y^2-\dfrac{1}{8}\)
=\(\dfrac{1}{8}\left(64y^2-1\right)\)
=\(\dfrac{1}{8}\left(8y-1\right)\left(8y+1\right)\)
b,\(\dfrac{1}{25}y^2-64m^2\)
=\(\left(\dfrac{1}{5}y-8m\right)\left(\dfrac{1}{5}y+8m\right)\)
B
1
12 tháng 9 2021
Ta có: \(\dfrac{\sqrt{15}-\sqrt{5}}{\sqrt{3}-1}+\sqrt{\left(2-\sqrt{5}\right)^2}-2\sqrt{5}\)
\(=\sqrt{5}+\sqrt{5}-2-2\sqrt{5}\)
=-2
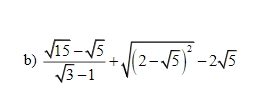
(2x² - 3x - 2) : (x - 2)
= (2x² - 4x + x - 2) : (x - 2)
= [(2x² - 4x) + (x - 2)] : (x - 2)
= [2x(x - 2) + (x - 2)] : (x - 2)
= (x - 2)(2x + 1) : (x - 2)
= 2x + 1
Ta có: