Cho A = 1 + 2 + 22 + 23 +...+ 29 và B = 5 . 28. So sánh A và B
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


S=1+2+22+...+29�=1+2+22+...+29
2S=2(1+2+22+...+210)2�=2(1+2+22+...+210)
2S=2+22+23+...+292�=2+22+23+...+29
2S−S=(2+22+23+...+210)−(1+2+22+...+29)
S=1+2+22+...+29�=1+2+22+...+29
2S=2(1+2+22+...+210)2�=2(1+2+22+...+210)
2S=2+22+23+...+292�=2+22+23+...+29
2S−S=(2+22+23+...+210)−(1+2+22+...+29)

a) Ta có \(\dfrac{23}{27}>\dfrac{23}{29};\dfrac{23}{29}>\dfrac{22}{29}\)
Vậy \(\dfrac{23}{27}>\dfrac{22}{29}\)
b) Ta có \(\dfrac{15}{25}=1-\dfrac{2}{5}\)
\(\dfrac{25}{49}=1-\dfrac{24}{49}\)
Vì \(\dfrac{2}{5}=\dfrac{24}{60}< \dfrac{24}{49}\)
Vậy \(\dfrac{15}{25}>\dfrac{25}{49}\)

1/
Tổng A là tổng các số hạng cách đều nhau 4 đơn vị.
Số số hạng: $(101-1):4+1=26$
$A=(101+1)\times 26:2=1326$
2/
$B=(1+2+2^2)+(2^3+2^4+2^5)+(2^6+2^7+2^8)+(2^9+2^{10}+2^{11})$
$=(1+2+2^2)+2^3(1+2+2^2)+2^6(1+2+2^2)+2^9(1+2+2^2)$
$=(1+2+2^2)(1+2^3+2^6+2^9)$
$=7(1+2^3+2^6+2^9)\vdots 7$

a) Có : 23/27>22/27
Mà 22/27>22/29
=> 23/27>22/29
b) Có : 12/25=24/50
24/50<24/49;24/49<25/49
=> 12/25<25/49
a,23/27>23/29
22/29<23/29
=>22/29<23/29<23/27
=>22/29<23/27
kl:....(kết luận)

a) Ta thấy 23/27>23/29 và 23/29>22/29 nên =>23/27>22/29
b) Ta thấy 25/74>1/3 và 1/3>12/37 nên 25/74>12/37
chúc bạn học tốt nha, nếu bạn muốn thì kết bạn với mình mình cho công thức luôn
B)25/74 và 12/37
Ta có 12/37=12*2/37*2
=24/74
=>25/74>24/74
Hay 25/74>12/37

a ) − 1 10 < 1. b ) 39 20 < 2. c ) − 1 20 > − 11 40 . d ) 5 9 > 2 9

Ta có A = \(\dfrac{1}{42}+\dfrac{1}{56}+\dfrac{1}{72}+\dfrac{1}{90}+\dfrac{1}{110}+\dfrac{1}{132}\)
= \(\dfrac{1}{6\cdot7}+\dfrac{1}{7\cdot8}+\dfrac{1}{8\cdot9}+\dfrac{1}{9\cdot10}+\dfrac{1}{10\cdot11}+\dfrac{1}{11\cdot12}\)
= \(\dfrac{1}{6}-\dfrac{1}{7}+\dfrac{1}{7}-\dfrac{1}{8}+\dfrac{1}{8}-\dfrac{1}{9}+\dfrac{1}{9}-\dfrac{1}{10}+\dfrac{1}{10}-\dfrac{1}{11}+\dfrac{1}{11}-\dfrac{1}{12}\)
= \(\dfrac{1}{6}-\dfrac{1}{12}=\dfrac{1}{12}\)
B = \(\dfrac{\dfrac{2}{29}-\dfrac{2}{39}+\dfrac{2}{49}}{\dfrac{23}{29}-\dfrac{23}{39}+\dfrac{23}{49}}=\dfrac{2\left(\dfrac{1}{29}-\dfrac{1}{39}+\dfrac{1}{49}\right)}{23\left(\dfrac{1}{29}-\dfrac{1}{39}+\dfrac{1}{49}\right)}=\dfrac{2}{23}\)
Lại có \(\dfrac{2}{23}>\dfrac{2}{24}=\dfrac{1}{12}\) hay A < B
Vậy A < B
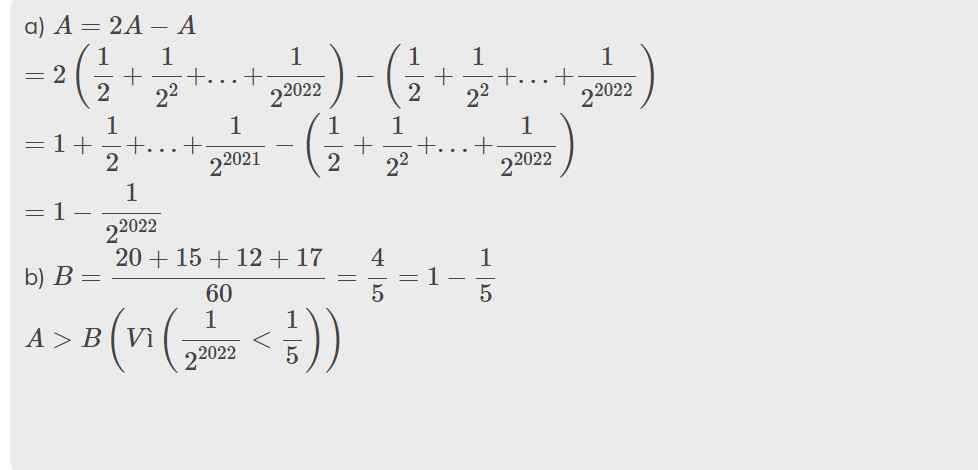
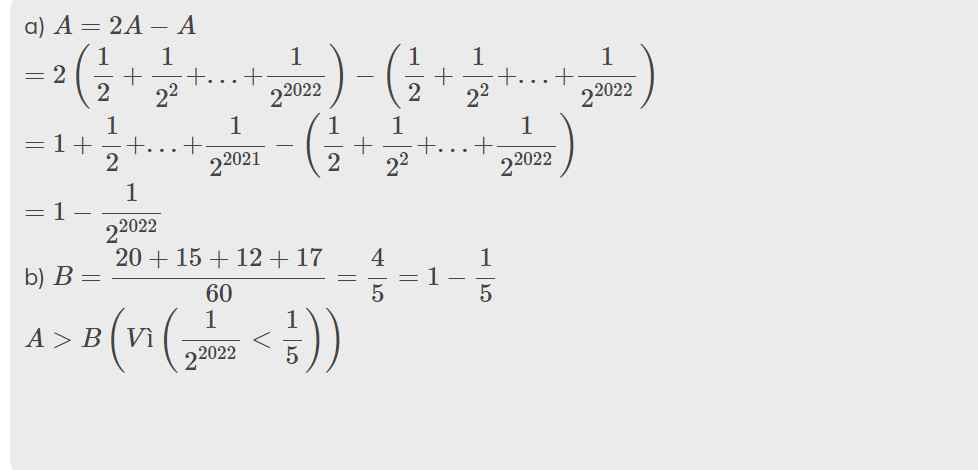
Giải thế này bạn nhé:
A = 1 + 2 + 22 + 23 + ... + 29 (1)
2A = 2 + 22 + 23 + ... + 29 + 210 (2)
Trừ từng vế của (2) cho (1) ta có:
2A - A = (2 + 22 + 23 + ... + 29 + 210) - (1 + 2 + 22 + 23 + ... + 29)= 210 - 1 hay A = 210 - 1
Còn: B = 5.28 = (22 + 1).28 = 210 + 28 Vậy B > A
k mk mk k lại
k mk nha
mk không bít
cảm ơn
hic