cho tam giác nhọn ABC,các đường cao AD, BE, CF ( D ∈ BC, E ∈ AC, F ∈ AB) cắt nhau tại H. Chứng minh rằng H cách đều 3 cạnh của tam giác DEF.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
27 tháng 7 2016
Trong 1 tam giác, 3 đường phân giác cắt nhau tại 1 điểm và điểm đó cách đều 3 cạnh của tam giác (điểm này gọi là tâm đường tròn nộ tiếp). Nối E -> F; E -> D ; D -> F. Ta sẽ chứng minh H là giao điểm 3 đường phân giác.
Ta chứng minh được ∆AFC ~ ∆AEB(g.g) => AF/AE = AC/AB => AF/AC = AE/AB. => ta chứng minh được ∆AEF ~ ∆ABC(c.g.c) => góc AEF = góc ABC, chứng minh tương tư ta được ∆CED ~ ∆CBA => góc CED = góc ABC => góc AEF = góc CED ( = góc ABC), ta có: góc FEB = 90º - góc AEF và góc BED = 90º - góc CED, mà góc AEF = góc CED => góc FEB = góc BED => BE là phân giác góc FED => EH là phân giác góc FED, chứng minh tương tự ta được DH là phân giác góc EDF và FH là phân giác góc EFD
=> đpcm
NH
8 tháng 6 2019
bạn chứng minh rõ DH là tia phân giác cho mình đc k, k rõ cho lắm
CM
20 tháng 9 2018
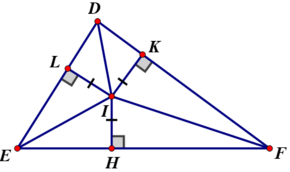
Gọi IH, IK, IL lần lượt là khoảng cách từ I đến EF, DF, DE.
Theo đề bài, điểm I cách đều ba cạnh của ΔDEF ⇒ IH = IK = IL
IL = IK ⇒ I cách đều hai cạnh của góc D ⇒ I nằm trên đường phân giác của góc D.
IH = IK ⇒ I cách đều hai cạnh của góc F ⇒ I nằm trên đường phân giác của góc F.
IH = IL ⇒ I cách đều hai cạnh của góc E ⇒ I nằm trên đường phân giác của góc E.
Từ 3 điều trên suy ra I là điểm chung của ba đường phân giác của tam giác DEF.
19 tháng 4 2017
Hướng dẫn:
I nằm trong ∆DEF và cách đều ba cạnh của tam giác nên I lần lượt thuộc phân giác của các góc ˆDD^, ˆEE^, ˆFF^
Vậy I là điểm chung của ba đường phân giác của tam giác DEF
19 tháng 4 2017
I nằm trong ∆DEF và cách đều ba cạnh của tam giác nên I lần lượt thuộc phân giác của các góc ˆDD^, ˆEE^, ˆFF^
Vậy I là điểm chung của ba đường phân giác của tam giác DEF
27 tháng 8 2016
I D E F
I nằm trong ∆DEF và cách đều ba cạnh của tam giác nên I lần lượt thuộc phân giác của các góc ∠D, ∠E , ∠F
Vậy I là điểm chung của ba đường phân giác của tam giác DEF
27 tháng 8 2016
mà hình như là đại học sư phạm rồi mà.bài dễ thế mà không biết làm à
Xét tứ giác BFHD có \(\widehat{BFH}+\widehat{BDH}=90^0+90^0=180^0\)
nên BFHD là tứ giác nội tiếp
Xét tứ giác CEHD có \(\widehat{CEH}+\widehat{CDH}=90^0+90^0=180^0\)
nên CEHD là tứ giác nội tiếp
Xét tứ giác AEHF có \(\widehat{AEH}+\widehat{AFH}=90^0+90^0=180^0\)
nên AEHF là tứ giác nội tiếp
Ta có: \(\widehat{FDH}=\widehat{FBH}\)(BFHD nội tiếp)
\(\widehat{EDH}=\widehat{ECH}\)(EHDC nội tiếp)
mà \(\widehat{FBH}=\widehat{ECH}\left(=90^0-\widehat{BAC}\right)\)
nên \(\widehat{FDH}=\widehat{EDH}\)
=>DH là phân giác của góc FDE
Ta có: \(\widehat{EFH}=\widehat{EAH}\)(AEHF nội tiếp)
\(\widehat{DFH}=\widehat{DBH}\)(BFHD nội tiếp)
mà \(\widehat{EAH}=\widehat{DBH}\left(=90^0-\widehat{ACD}\right)\)
nên \(\widehat{EFH}=\widehat{DFH}\)
=>FH là phân giác của góc EFD
Xét ΔEFD có
DH,FH là các đường phân giác
DH cắt FH tại H
Do đó: H là tâm đường tròn nội tiếp của ΔEFD
hay H cách đều ba cạnh của ΔEFD