cko tam giác AOB vuông tại O với đường cao OM .Hãy giải thích vì sao ta có đẳng thức AB.OM=OA.OB
Cko tam giác ABC và đường trung tuyên AM .Chứng minh SAMB=SAMC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
25 tháng 5 2018
Ta có cách tính diện tích ΔAOB với đường cao OM và cạnh đáy AB:
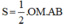
Ta lại có cách tính diện tích ΔAOB vuông với hai cạnh góc vuông OA, OB là:
PT
1
CM
3 tháng 9 2019
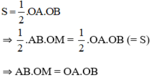
Kẻ đường cao AH
Ta có: SAMB = 0.5.BM.AH
SAMC = 0.5.CM.AH
Mà BM = CM (gt)
Þ SAMB = SAMC (ĐPCM)
PT
1
CM
1 tháng 5 2019
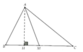
Kẻ đường cao AH.
Ta có:
Mà BM = CM (vì AM là trung tuyến)
⇒ SAMB = SAMC (đpcm).
4 tháng 9 2023
a: Xét tứ giác ADHP có
AD//HP
AP//HD
góc PAD=90 độ
Do đó: ADHP là hình chữ nhật
=>AH=DP
b: ΔABC vuông tại A có AM là đường trung tuyến
nên MA=1/2BC=MC=MB
Xét ΔMAC có MA=MC
nên ΔMAC cân tại M
c: góc QAP+góc QPA
=góc MAC+góc APD
=góc MCA+góc AHD
=góc ACB+góc ABC=90 độ
=>ΔQAP vuông tại Q
24 tháng 5 2022
a: Xét ΔAHB vuông tại H và ΔAKC vuông tại K có
AB=AC
góc HAB chung
Do đó: ΔAHB=ΔAKC
Suy ra: HB=KC
Xét ΔKBC vuông tại K và ΔHCB vuông tại H có
BC chung
KC=HB
Do đó: ΔKBC=ΔHCB
Suy ra: \(\widehat{OCB}=\widehat{OBC}\)
=>ΔOBC cân tại O
=>OB=OC
mà AB=AC
nên AO là đường trung trực của BC
hay AO\(\perp\)BC
b: Xét ΔAOB và ΔAOC có
AO chung
OB=OC
AB=AC
Do đó ΔAOB=ΔAOC
SUy ra: \(\widehat{OAB}=\widehat{OAC}=30^0\)
=>\(\widehat{BAC}=60^0\)
hay ΔABC đều
c: Đề sai rồi bạn
mỗi câu là một bài nha
câu 2
Dựng AH là đường cao của ΔABC, khi đó ΔABM,ΔAMC chung chiều cao AH. Ta có:
SAMB=12BM.AH
SAMC=12CM.AH
mà BM=CMBM=CM (vì AM là đường trung tuyến)
Vậy SAMB=SAMC.
S là diện -.-