Tính lực tổng hợp của hai lực F_{1} = 8N F_{2} = 6 N
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
15 tháng 11 2021
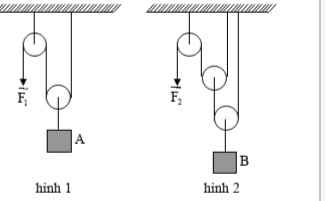
a)Gọi trọng lượng của ròng rọc 2 là \(P_1\)
Ở hình 1: \(F_1=\dfrac{P_A+P_1}{2}\Rightarrow P_1=2F_1-P_A\) (1)
Ở hình 2: \(F_2=\dfrac{\dfrac{P_B+P_1}{2}+P_1}{2}=\dfrac{P_B+3P_1}{4}\)
\(\Rightarrow P_1=\dfrac{4F_2-P_B}{3}\) (2)
Từ (1) và (2) \(\Rightarrow2F_1-P_A=\dfrac{4F_2-P_B}{3}\)
Mà \(P_A=P_B\); \(F_1=1000N;F_2=700N\)
\(\Rightarrow P_A=1600N\)
Lại có: \(P_A=10m_A\Rightarrow m_A=160kg\)\
b)Ròng rọc ở hệ thống 2.
Thấy 2 ròng rọc động\(\Rightarrow\) Lợi 4 lần về lực và thiệt 4 lần về đường đi.
\(\Rightarrow H=\dfrac{P_B\cdot h}{F_2\cdot S}=\dfrac{P_B\cdot h}{F_2\cdot4h}\cdot100\%\approx57\%\)
HQ
Hà Quang Minh
Giáo viên
5 tháng 11 2023
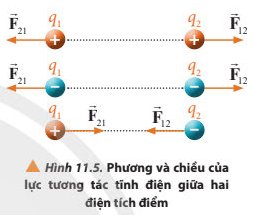
Các cặp lực \(\overrightarrow {{F_{12}}} \) và \(\overrightarrow {{F_{21}}} \) có là những cặp lực cân bằng vì theo định luật III Newton ta có: Khi một vật tác dụng lực lên vật thể thứ hai, vật thứ hai sẽ tác dụng một lực cùng độ lớn và ngược chiều về phía vật thứ nhất.
20 tháng 12 2016
Trong trường hợp này do vật chuyển động thẳng đều nên lực tác dụng vào vật sẽ là 2 lực cân bằng. Lực tác dụng là 35N giúp vật chuyển động nên lực kéo cân bằng và ngược chiều với lực này. Do vậy lực ma sát có độ lớn là:
Fms = Ftác dụng = 35N
25 tháng 1 2018
Giả sử f(x)=ax2+bx+cf(x)=ax2+bx+c (do đề bài cho là đa thức bậc hai)
Suy ra
f(x)−f(x−1)=ax2+bx+c−a(x−1)2−b(x−1)−c=2ax+a+bf(x)−f(x−1)=ax2+bx+c−a(x−1)2−b(x−1)−c=2ax+a+b
Mà f(x)−f(x−1)=xf(x)−f(x−1)=x
⇒2ax+a+b=x⇒2ax+a+b=x
Do đó a+b=0a+b=0 và a=1/2a=1/2 từ đó ta suy ra a=1/2;b=−1/2a=1/2;b=−1/2
Do đó f(x)=x22−x2+cf(x)=x22−x2+c
f(n)=1+2+3+...+nf(n)=1+2+3+...+n
Áp dụng điều ta vừa chứng minh được thì:
f(1)−f(0)=1f(1)−f(0)=1
f(2)−f(1)=2f(2)−f(1)=2
....
f(n)−f(n−1)=nf(n)−f(n−1)=n
Do đó
1+2+...+n=f(1)−f(0)+f(2)−f(1)+...+f(n)−f(n−1)=f(n)−f(0)=n22−n2=n(n−1)2
12 tháng 3 2018
Suy ra
f(x)−f(x−1)=ax2+bx+c−a(x−1)2−b(x−1)−c=2ax+a+bf(x)−f(x−1)=ax2+bx+c−a(x−1)2−b(x−1)−c=2ax+a+b
Mà f(x)−f(x−1)=xf(x)−f(x−1)=x
⇒2ax+a+b=x⇒2ax+a+b=x
Do đó a+b=0a+b=0 và a=1/2a=1/2 từ đó ta suy ra a=1/2;b=−1/2a=1/2;b=−1/2
Do đó f(x)=x22−x2+cf(x)=x22−x2+c
f(n)=1+2+3+...+nf(n)=1+2+3+...+n
Áp dụng điều ta vừa chứng minh được thì:
f(1)−f(0)=1f(1)−f(0)=1
f(2)−f(1)=2f(2)−f(1)=2
....
f(n)−f(n−1)=nf(n)−f(n−1)=n
Do đó
1+2+...+n=f(1)−f(0)+f(2)−f(1)+...+f(n)−f(n−1)=f(n)−f(0)=n22−n2=n(n−1)2
:3
6 tháng 12 2021
Định luật ll Niu tơn ta có:
\(\overrightarrow{F}+\overrightarrow{F_{ms}}=m\cdot\overrightarrow{a}\)
\(\Rightarrow a=\dfrac{F_{ms}}{m}=\dfrac{\mu mg}{m}=\mu\cdot g=0,1\cdot10=1\)m/s2
Độ lớn lực kéo:
\(F=F_{ms}+m\cdot a=0,1\cdot5\cdot1000\cdot10+5\cdot1000\cdot1=10000N\)
Nếu cùng chiều: 𝐹 = 14 N F=14N. Nếu ngược chiều: 𝐹 = 2 N F=2N. Nếu vuông góc: 𝐹 = 10 N F=10N. Bạn kiểm tra xem bài có nói hướng không nhé!