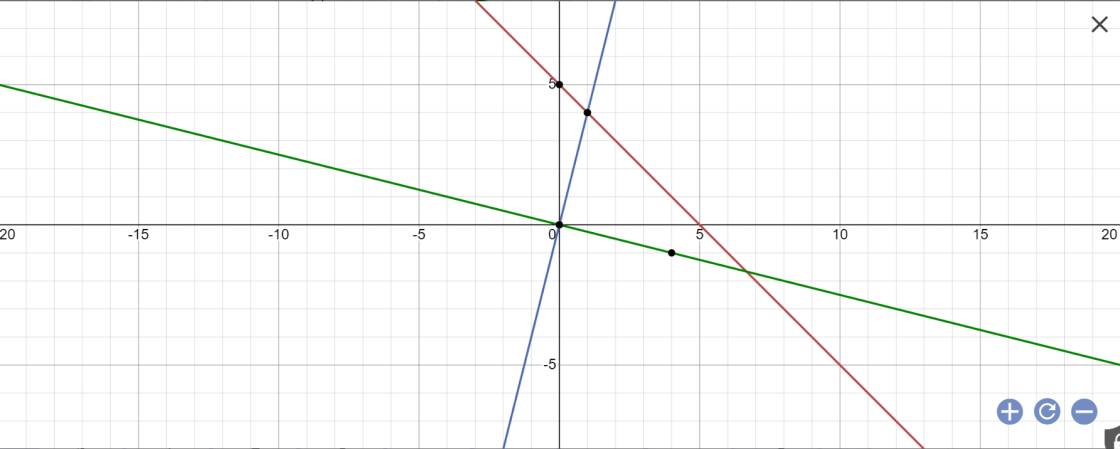
a) Vẽ đồ thị hàm số sau trên 1 hê trục tọa độ:
\(y=-x+5\) (1)
\(y=4x\) (2)
\(y=\dfrac{1}{4}x\) (3)
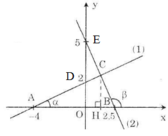
b) Gọi giao điểm của đường thẳng có phương trình (1) có các đường thẳng với phương trình (2) và (3) lần lượt là A và B. Tìm tọa độ các điểm A, B.
c) TAm giác AOB là tam giác gì? Vì sao?
d) Tính S tam giác AOB.
Mình mọng mọi người giúp mình bài này. Mình rất gấp

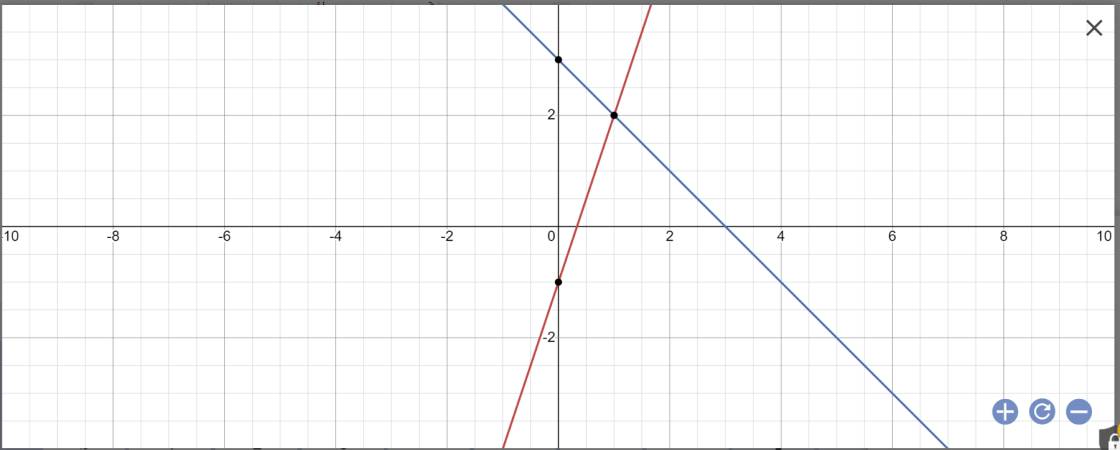
a) Bạn tự vẽ.
b) Lập PT hoành độ giao điểm:
(d1) giao (d2): \(-x-5=\frac{1}{4}x\Leftrightarrow x=-4\) thay vào (d1) được y = -1
Vậy: \(A\left(-4;-1\right)\). Tương tự tìm được \(B\left(-1;-4\right)\)
c) Ta có: \(AB=\sqrt{\left(x_B-x_A\right)^2+\left(y_B+y_A\right)^2}=\sqrt{\left(-1+4\right)^2+\left(-4+1\right)^2}=3\sqrt{2}\)
\(OA=\sqrt{x^2_A+y^2_A}=\sqrt{4^2+1^2}=17;OB=\sqrt{x^2_B+y^2_B}=\sqrt{1^2+4^2}=\sqrt{17}\)
=> OAB là tam giác cân.
d) Gọi OAB là đường cao hạ từ điểm O xuống AB (H thuộc AB)
Vì tam giác OAB cân tại O nên \(AH=HB=\frac{1}{2}AB=\frac{3\sqrt{2}}{2}\)
\(OH=\sqrt{OA^2-BH^2}=\sqrt{17-\left(\frac{3\sqrt{2}}{2}\right)^2}=\frac{5\sqrt{2}}{2}\)
\(S_{ABC}=\frac{1}{2}AB.OH=\frac{1}{2}.3\sqrt{2}.\frac{5\sqrt{2}}{2}=\frac{15}{2}\)