- Cho tam giác cân ABC . Góc A = 20o . Cạnh BC = 2 cm Trên tia AB dựng điểm D sao cho góc ACD = 10o . Tính AD = ? cm
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
KV
10 tháng 1
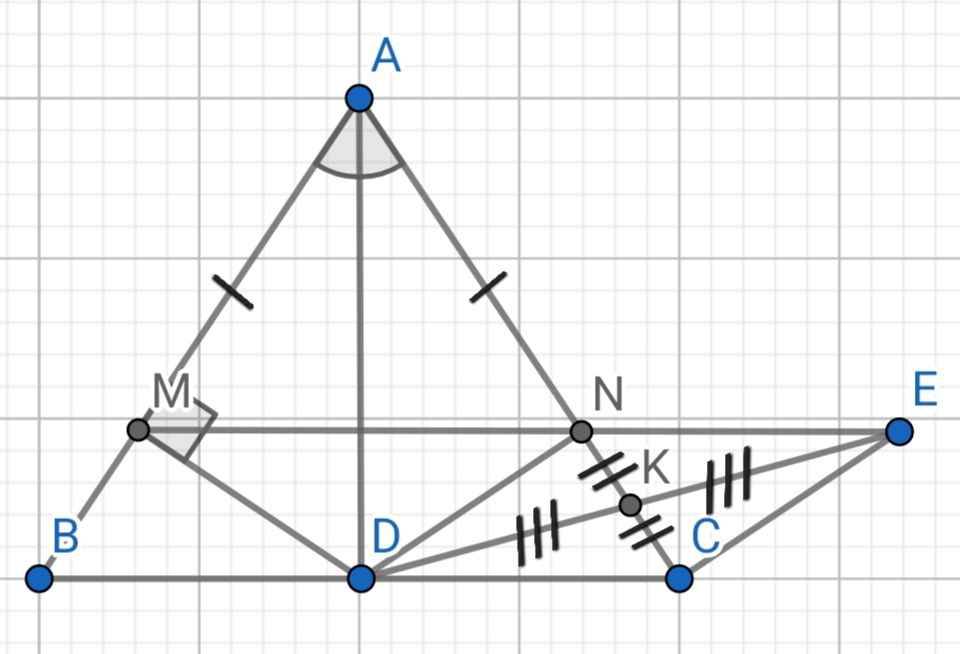a) Do AD là tia phân giác của ∠BAC (gt)
⇒ ∠BAD = ∠CAD
Do ∆ABC cân tại A
⇒ AB = AC
Xét ∆ABD và ∆ACD có:
AB = AC (cmt)
∠BAD = ∠CAD (cmt)
AD là cạnh chung
⇒ ∆ABD = ∆ACD (c-g-c)
⇒ BD = CD
⇒ D là trung điểm của BC (1)
Do ∆ABD = ∆ACD (cmt)
⇒ ∠ADB = ∠ADC (hai góc tương ứng)
Mà ∠ADB + ∠ADC = 180⁰ (kề bù)
⇒ ∠ADB = ∠ADC = 180⁰ : 2 = 90⁰
⇒ AD ⊥ BC (2)
Từ (1) và (2) ⇒ AD là đường trung trực của BC
b) Sửa đề: Chứng minh ∆ADM = ∆ADN
Do ∠BAD = ∠CAD (cmt)
⇒ ∠MAD = ∠NAD
Xét ∆ADM và ∆ADN có:
AD là cạnh chung
∠MAD = ∠NAD (cmt)
AM = AN (gt)
⇒ ∆ADM = ∆ADN (c-g-c)
⇒ ∠AMD = ∠AND = 90⁰ (hai góc tương ứng)
⇒ DN ⊥ AN
⇒ DN ⊥ AC
d) Do K là trung điểm của CN (gt)
⇒ CK = KN
Xét ∆DKC và ∆EKN có:
CK = KN (cmt)
∠DKC = ∠EKN (đối đỉnh)
KD = KE (gt)
⇒ ∆DKC = ∆EKN (c-g-c)
⇒ ∠KDC = ∠KEN (hai góc tương ứng)
Mà ∠KDC và ∠KEN là hai góc so le trong
⇒ EN // CD
⇒ EN // BC (3)
∆AMN có:
AM = AN (gt)
⇒ ∆AMN cân tại A
⇒ ∠AMN = (180⁰ - ∠MAN) : 2
= (180⁰ - ∠BAC) : 2 (4)
∆ABC cân tại A (gt)
⇒ ∠ABC = (180⁰ - ∠BAC) : 2 (5)
Từ (4) và (5) ⇒ ∠AMN = ∠ABC
Mà ∠AMN và ∠ABC là hai góc đồng vị
⇒ MN // BC (6)
Từ (3) và (6) kết hợp với tiên đề Euclide ⇒ M, N, E thẳng hàng
LD
23 tháng 6 2017
Trên mặt phẳng bờ là đường thẳng BC chứa điểm A vẽ \(\Delta EBC\)đều. Gọi H là giao điểm của AE và CD.
Xét \(\Delta ABC\)cân tại A có \(\widehat{BAC}=20^o\)
\(\Rightarrow\)\(\widehat{ABC}=\widehat{ACB}=80^o\)
Ta có:
\(\widehat{ECD}=\widehat{ACB}-\widehat{ECB}-\widehat{ACD}\)
\(\widehat{ECD}=80^o-60^o-10^o=10^o\)
Xét \(\Delta AEB\) và \(\Delta AEC\)ta có:
AE là cạnh chung
AB = AC ( \(\Delta ABC\)cân tại A)
EB = EC ( \(\Delta EBC\)đều)
\(\Rightarrow\)\(\Delta AEB=\Delta AEC\left(c-c-c\right)\)
\(\Rightarrow\)\(\widehat{EAB}=\widehat{EAC}\)(2 góc tương ứng)
\(\Rightarrow\)AE là tia phân giác của \(\widehat{BÃC}\)
\(\Rightarrow\)\(\widehat{EAB}=\widehat{EAC}=\frac{\widehat{BAC}}{2}=\frac{20^o}{2}=10^o\)
Ta có:
\(\widehat{HAC}=\widehat{HCA}\left(=10^o\right)\)
\(\Rightarrow\)\(\Delta HAC\)cân tại H
\(\Rightarrow\)\(HA=HC\)
Xét \(\Delta HAD\)và \(\Delta HCE\) TA CÓ:
\(HA=HC\left(cmt\right)\)
\(\widehat{AHD}=\widehat{CHE}\) ( 2 góc đối đỉnh)
\(\widehat{DAH}=\widehat{ECH}\left(=10^o\right)\)
\(\Rightarrow\)\(\Delta HAD=\Delta HCE\left(g-c-g\right)\)
\(\Rightarrow\)\(AD=EC\)(2 cạnh tương ứng)
Mà \(EC=BC\)( \(\Delta EBC\)đều)
Nên \(AD=BC\)
Mặt khác \(BC=2cm\left(gt\right)\)
\(\Rightarrow\)\(AD=2cm\)
11 tháng 6 2019
a, xét tam giácABH và tam giác ACH có : AH chung
góc CAH = góc BAH do AH là phân giác của góc A (gt)
AB = AC do tam giác ABC cân tại A (gt)
=> tam giác ABH = tam giác ACH (c-g-c)
b, AB = AC (câu a)
mà AB = AD (gt)
=> AC = AD
=> tam giác ACD cân tại A (đn)
25 tháng 3 2023
Sửa đề: AC=7,5
a: Sửa đề: ΔABC đồng dạng với ΔCBD
Xét ΔABC và ΔCBD có
BA/BC=CB/BD
góc B chung
=>ΔABC đồng dạng với ΔCBD
b: ΔABC đồng dạng với ΔCBD
=>AC/CD=AB/CB
=>7,5/CD=6/9=2/3
=>CD=11,25(cm)
2 tháng 1 2022
b: Xét ΔAEC và ΔAED có
AC=AD
\(\widehat{CAE}=\widehat{DAE}\)
AE chung
Do đó: ΔAEC=ΔAED
Suy ra: EC=ED
21 tháng 9 2016
AD =2cm
muốn tính AD dựa vào dg tron ngoai tiep cua tg ABC
( chỉ vì bai nay ma tui phai thi lai v2 vi muon 300đ)