toán nâng cao ' part 1'
bài 1:
Tìm 2 số tự nhiên a,b sao cho ƯCLN(a,b)=4 và a+b=48
bài 2 : tìm số tự nhiên n sao cho:
a) n2 + 3n + 1 chia hết cho n+1
b) n2 + 6 chia hết cho n+2
bài 3 :
a) với mọi số tự nhiên a,b nếu 5a + 3b và 13a + 8b cùng chia hết cho 2021 thì a và b cũng chia hết cho 2021
b) cho A = \(3+3^2+3^3+...+3^{100}\) tìm \(n\in N\) biết 2A +3=\(3^n\)
c) cho A = \(1-3+3^2-3^3+3^4-...+3^{98}-3^{99}+3^{100}\) . Tìm số dư trong phép chia S : 4
bài 4 :
tìm số nguyên tố p sao cho p+4 và p+8 đều là các số nguyên tố

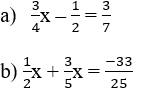


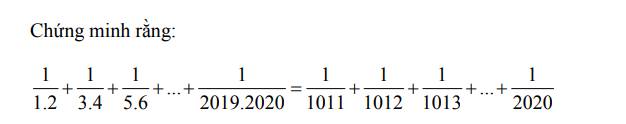



 Hép, đây là toán nâng cao ;-;
Hép, đây là toán nâng cao ;-;
Bài 2:
a: \(n^2+3n+1⋮n+1\)
=>\(n^2+n+2n+2-1⋮n+1\)
=>\(-1⋮n+1\)
mà n+1>=1(do n là số tự nhiên)
nên n+1=1
=>n=0
b:
\(n^2+6⋮n+2\)
=>\(n^2-4+10⋮n+2\)
=>\(10⋮n+2\)
mà n+2>=2(Do n là số tự nhiên)
nên \(n+2\in\left\{2;5;10\right\}\)
=>\(n\in\left\{0;3;8\right\}\)
Bài 4:
TH1: p=3
p+4=3+4=7; p+8=3+8=11
=>Nhận
TH2: p=3k+1
\(p+8=3k+1+8=3k+9=3\left(k+3\right)⋮3\)
=>Loại
TH3: p=3k+2
\(p+4=3k+2+4=3k+6=3\left(k+2\right)⋮3\)
=>Loại
Vậy: p=3
Bài 1
Vì ƯCLN (a,b) = 4 nên a = 4m , b = 4n (m,n \(\in\) N*) , (m,n) = 1
Thay a = 4m, b = 4n vào a + b, ta có:
4m + 4n = 48
4 ( m + n ) = 48
m + n = 48 : 4
m + n = 12
Mà m,n \(\in\) N* và ( m,n ) = 1 nên ta có bảng sau:
Vậy các cặp (a,b) cần tìm là: (4,44);(44,4);(20,28);(28,20)
(Các bài khác bn xem của người khác nhé, mik chx kịp làm)