K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
9 tháng 5 2023
a: Xét ΔAHB vuông tại H và ΔDAB vuông tại A có
góc ABH chung
=>ΔAHB đồng dạng vơi ΔDAB
b: \(BD=\sqrt{12^2+16^2}=20\left(cm\right)\)
BH=12^2/20=7,2cm
AH=12*16/20=9,6cm
18 tháng 11 2023
a: ABCD là hình chữ nhật
=>\(BD^2=BA^2+BC^2\)
=>\(BD^2=5^2+12^2=169\)
=>BD=13(cm)
b: Xét ΔADB vuông tại A có AH là đường cao
nên \(AH\cdot BD=AB\cdot AD\)
=>\(AH\cdot13=5\cdot12=60\)
=>\(AH=\dfrac{60}{13}\left(cm\right)\)
c: \(\widehat{HDK}+\widehat{HBC}=90^0\)(ΔBDC vuông tại C)
\(\widehat{HIB}+\widehat{HBI}=90^0\)(ΔHBI vuông tại H)
mà \(\widehat{HBC}=\widehat{HBI}\left(I\in BC\right)\)
nên \(\widehat{HDK}=\widehat{HIB}\)
Xét ΔHDK vuông tại H và ΔHIB vuông tại H có
\(\widehat{HDK}=\widehat{HIB}\)
Do đó: ΔHDK đồng dạng với ΔHIB
=>\(\dfrac{HD}{HI}=\dfrac{HK}{HB}\)
=>\(HD\cdot HB=HK\cdot HI\)(1)
Xét ΔABD vuông tại A có AH là đường cao
nên \(AH^2=HD\cdot HB\left(2\right)\)
Từ (1) và (2) suy ra \(AH^2=HK\cdot HI\)
14 tháng 6 2021
từ điểm N hạ \(ON\perp DC\)
ABCD là hình chữ nhật=>\(\left\{{}\begin{matrix}AB=DC=4cm\\AD=BC=2cm\end{matrix}\right.\)
mà \(ABCD\) là hình chữ nhật \(=>BC\perp CD=>BC//ON\)
mà \(NM=NB=>ON\) là đường trung bình \(\Delta MBC\)
\(=>ON=\dfrac{1}{2}BC=\dfrac{1}{2}.2=1cm\)
do ON là đường trung bình \(=>MO=OC=\dfrac{1}{2}MC\)
mà \(MC=DM=\dfrac{1}{2}DC=\dfrac{1}{2}.4=2cm\)
\(=>MO=\dfrac{1}{2}MC=\dfrac{1}{2}.2=1cm\)
\(=>OD=DM+OM=1+2=3cm\)
xét \(\Delta DNO\) vuông tại O\(=>DN=\sqrt{ON^2+DO^2}=\sqrt{3^2+1^2}=\sqrt{10}cm\)
CM
18 tháng 11 2018
Các em tự thực hành đo. Kết quả là:
- Thước đo góc này sai.
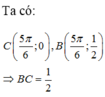
Độ dài đường gấp khúc ABC là 14cm
=>AB+BC=14
mà AB=CD
nên BC+CD=14
Độ dài đường gấp khúc DABC là 20cm
=>DA+AB+BC=20
=>DA+CD+BC=20
=>DA=20-14=6(cm)
mà DA=BC
nên BC=6cm
CD=14-BC=14-6=8(cm)