lời giải kèm hình . giúp mik vs ạ mik sẽ kb ạ
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
24 tháng 3 2023
a: Xét ΔAHB vuông tạiH và ΔCAB vuông tại A có
góc B chung
=>ΔAHB đồng dạng với ΔCAB
b: AH=3*4/5=2,4cm
c: ΔABC vuông tại A có HA là đường cao
nên AB^2=BH*BC
14 tháng 4 2023
a: Xét ΔAIB vuông tại I và ΔAEC vuông tại E có
góc A chung
=>ΔAIB đồng dạng với ΔAEC
=>AI/AE=AB/AC
=>AI/AB=AE/AC
b: Xét ΔAIE và ΔABC có
AI/AB=AE/AC
góc A chung
=>ΔAIE đồg dạng với ΔABC
11 tháng 3 2022
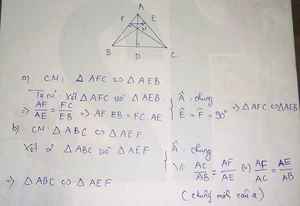
a) Xét \(\Delta ABE\) và \(\Delta ACF:\)
\(\widehat{A}chung.\\ \widehat{AEB}=\widehat{AFC}\left(=90^o\right).\\ \Rightarrow\Delta ABE\sim\Delta ACF\left(g-g\right).\)
b) Xét \(\Delta AEF\) và \(\Delta ABC:\)
\(\widehat{A}chung.\\ \dfrac{AE}{AB}=\dfrac{AF}{AC}\left(\Delta ABE\sim\Delta ACF\right).\\ \Rightarrow\Delta AEF\sim\Delta ABC\left(c-g-c\right).\)
11 tháng 3 2022
TK
https://hoc24.vn/cau-hoi/bai-1-cho-d-abc-cac-duong-cao-be-va-cf-cat-nhau-tai-ha-chung-minh-tam-giac-abe-dong-dang-voi-tam-giac-afcb-chung-minh-tam-giac-aef-dong-dang-voi.5075521880097
27 tháng 1 2022
a: Xét ΔABC vuông tại A và ΔHBA vuông tại H có
\(\widehat{ABC}\) chung
Do đó: ΔABC\(\sim\)ΔHBA
b: XétΔABC vuông tại A có AH là đường cao
nên \(AH^2=BH\cdot CH\)
c: Vì \(AH^2=BH\cdot CH=4\cdot16=64\left(cm\right)\)
nên AH=8cm
Xét tứ giác ADHE có
\(\widehat{ADH}=\widehat{AEH}=\widehat{DAE}=90^0\)
Do đó: ADHE là hình chữ nhật
Suy ra: AH=DE=8(cm)
27 tháng 1 2022
a, Xét tam giác ABC và tam giác HBA ta có :
^BAC = ^BHA = 900
^B _ chung
Vậy tam giác ABC ~ tam giác HBA ( g.g )
b, Xét tam giác ABH và tam giác CAH ta có :
^AHB = ^CHA = 900
^ABH = ^CAH ( cùng phụ ^BAC )
Vậy tam giác ABH~ tam giác CAH (g.g )
=> AH/CH=BH/AH => AH^2 = CH.BH
c, Ta có : AH = 2 . 4 = 8 cm
Xét tứ giác ADHE có :
^A = ^ADH = ^AEH = 900
Vậy tứ giác ADHE là hcn
=> AH = DE = 8 cm
d, Ta có : \(\dfrac{S_{AMH}}{S_{ABC}}=\left(\dfrac{AH}{AC}\right)^2\)
Xét tam giác AHC và tam giác ABC
^AHC = ^BAC = 900
^HAC = ^B ( cùng phụ ^BAM )
Vậy tam giác AHC ~ tam giác BAC ( g.g)
=> AC / BC = HC/AC => AC^2 = HC ( HB + HC )
=> AC = 4 . 5 = 20 cm
Thay vào ta được : \(\left(\dfrac{AH}{AC}\right)^2=\left(\dfrac{8}{20}\right)^2=\dfrac{64}{400}=\dfrac{4}{25}\)
14 tháng 4 2023
a: Xét ΔBEC và ΔAEFcó
góc BEC=góc AEF
góc ECB=góc EFA
=>ΔBEC đồng dạng với ΔAEF
b: Xét ΔFEA và ΔFCD có
góc FEA=góc FCD
góc F chung
=>ΔFEA đồng dạng với ΔFCD
a: Xét ΔABD vuông tại A và ΔABC vuông tại A có
AB chung
AD=AC
Do đó: ΔABD=ΔABC
b: ΔABD=ΔABC
=>BD=BC
ΔABD=ΔABC
=>\(\widehat{ABD}=\widehat{ABC}\)
=>\(\widehat{MBC}=\widehat{MBD}\)
Xét ΔMBC và ΔMBD có
MB chung
\(\widehat{MBC}=\widehat{MBD}\)
BC=BD
Do đó: ΔMBC=ΔMBD