Question

[Hoàng]

Câu 1 giải các phương trình sau bằng cách đưa về phương trình tích

a) x² + 7x = 0                                         b) (3x + 2)² - 4x²= 0

c) 2x( x + 6)+5(x + 6) = 0                       d) x(3x + 5) - 6x - 10 = 0

Câu 2 giải các phương trình sau bằng cách đưa về phương trình tích

a) (2x - 3)² = (x + 7)²                            b) x²  - 9 = 3(x + 3)

c) x² - x = - 2x + 2                                 d) x² - 3x = 2x - 6

Câu 3 giải các phương trình sau bằng cách đưa về phương trình tích

a) 3x² - 11x - 6 = 0                               b) - 2x² + 5x + 3= 0

c) x³ + 2x - 3 = 0                                  d) x³ + 8 = x² - 4

GIẢI CHI TIẾT GIÚP MÌNH NHÉ, CẢM ƠN RẤT NHIỀU!

Answer 1

[Nguyễn Lê Phước Thịnh]

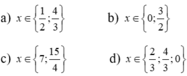
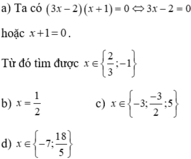
Câu 1:

a: \(x^2+7x=0\)

=>x(x+7)=0

=>\(\left[{}\begin{matrix}x=0\\x+7=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=-7\end{matrix}\right.\)

b: \(\left(3x+2\right)^2-4x^2=0\)

=>\(\left(3x+2+2x\right)\left(3x+2-2x\right)=0\)

=>(x+2)(5x+2)=0

=>\(\left[{}\begin{matrix}x+2=0\\5x+2=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-2\\x=-\dfrac{2}{5}\end{matrix}\right.\)

c: \(2x\left(x+6\right)+5\left(x+6\right)=0\)

=>(x+6)(2x+5)=0

=>\(\left[{}\begin{matrix}x+6=0\\2x+5=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-6\\x=-\dfrac{5}{2}\end{matrix}\right.\)

d: \(x\left(3x+5\right)-6x-10=0\)

=>x(3x+5)-2(3x+5)=0

=>(3x+5)(x-2)=0

=>\(\left[{}\begin{matrix}3x+5=0\\x-2=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{5}{3}\\x=2\end{matrix}\right.\)

Câu 2:

a: \(\left(2x-3\right)^2=\left(x+7\right)^2\)

=>\(\left(2x-3\right)^2-\left(x+7\right)^2=0\)

=>(2x-3-x-7)(2x-3+x+7)=0

=>(x-10)(3x+4)=0

=>\(\left[{}\begin{matrix}x-10=0\\3x+4=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=10\\x=-\dfrac{4}{3}\end{matrix}\right.\)

b: \(x^2-9=3\left(x+3\right)\)

=>\(\left(x-3\right)\left(x+3\right)-3\left(x+3\right)=0\)

=>(x+3)(x-6)=0

=>\(\left[{}\begin{matrix}x+3=0\\x-6=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-3\\x=6\end{matrix}\right.\)

c: \(x^2-x=-2x+2\)

=>\(x\left(x-1\right)=-2\left(x-1\right)\)

=>(x-1)(x+2)=0

=>\(\left[{}\begin{matrix}x-1=0\\x+2=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=1\\x=-2\end{matrix}\right.\)

d: \(x^2-3x=2x-6\)

=>\(x\left(x-3\right)=2\left(x-3\right)\)

=>(x-3)(x-2)=0

=>\(\left[{}\begin{matrix}x-3=0\\x-2=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=3\\x=2\end{matrix}\right.\)

Câu 3:

b: \(-2x^2+5x+3=0\)

=>\(-2x^2+6x-x+3=0\)

=>-2x(x-3)-(x-3)=0

=>(x-3)(-2x-1)=0

=>(x-3)(2x+1)=0

=>\(\left[{}\begin{matrix}x-3=0\\2x+1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=3\\x=-\dfrac{1}{2}\end{matrix}\right.\)

c: \(x^3+2x-3=0\)

=>\(x^3-x+3x-3=0\)

=>\(x\left(x^2-1\right)+3\left(x-1\right)=0\)

=>\(x\left(x-1\right)\left(x+1\right)+3\left(x-1\right)=0\)

=>\(\left(x-1\right)\left(x^2+x+3\right)=0\)

mà \(x^2+x+3=\left(x+\dfrac{1}{2}\right)^2+\dfrac{11}{4}>=\dfrac{11}{4}>0\forall x\)

nên x-1=0

=>x=1

d: \(x^3+8=x^2-4\)

=>\(\left(x+2\right)\left(x^2-2x+4\right)-\left(x+2\right)\left(x-2\right)=0\)

=>\(\left(x+2\right)\left(x^2-2x+4-x+2\right)=0\)

=>\(\left(x+2\right)\left(x^2-3x+6\right)=0\)

mà \(x^2-3x+6=x^2-3x+\dfrac{9}{4}+\dfrac{15}{4}=\left(x-\dfrac{3}{2}\right)^2+\dfrac{15}{4}>=\dfrac{15}{4}>0\forall x\)

nên x+2=0

=>x=-2

Answer 2

[Anna]

Oguo