Cho sinx=5/8 với x thuộc (5π/2;3π). Tính sinx (x+π/3)
Hộ em với ạ😥
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
31 tháng 10 2017
Đáp án đúng: C
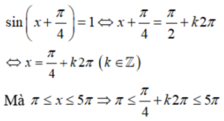
⇔ 3 4 ≤ k ≤ 19 8 ⇒ k ∈ 1 ; 2
Vậy phương trình có 2 nghiệm trong π ; 5 π
CM
14 tháng 3 2017
Đáp án B
PT sin x + π 4 = 1 ⇔ x + π 4 = π 2 + k 2 π ⇔ x = π 4 + k 2 π
Ta thấy π 4 + k 2 π ∈ π ; 5 π ⇔ k ∈ 1 ; 2 ⇒ P T có hai nghiệm thuộc π ; 5 π
CM
15 tháng 7 2017
Đáp án D.
Phương trình tương đương với 2017 sin x = sin x + 1 + sin 2 x .
Đặt t = sin x , t ∈ − 1 ; 1 thì phương trình trở thành 2017 t = t + 1 + t 2 .
⇔ t . l n 2017 − l n t + 1 + t 2 = 0 , do t + 1 + t 2 > t 2 + t = t + t ≥ 0, ∀ t .
Xét hàm số f ( t ) = t . ln 2017 − ln t + 1 + t 2 trên − 1 ; 1 .
Đạo hàm
f ' ( t ) = t 2 + 1 . ln 2017 − 1 1 + t 2 > ln 2017 − 1 1 + t 2 > 0, ∀ t ∈ − 1 ; 1 .
Suy ra hàm số f(t) đồng biến trên − 1 ; 1 . Mà f 0 = 0 nên phương trình f t = 0 có duy nhất một nghiệm t=0.
Như vậy sin x = 0 ⇔ x = k π , ( k ∈ ℤ ) . Vì x ∈ − 5 π ; 2017 π nên − 5 ≤ k ≤ 2017.
Vậy có 2017 – – 5 + 1 = 2023 giá trị k nên phương trình đã cho có 2023 nghiệm thực trên − 5 π ; 2017 π
CM
16 tháng 3 2018
a) 
f′(x) > 0 trên khoảng (-4; 0) và f’(x) < 0 trên khoảng (0; 4).
Hàm số đạt cực đại tại x = 0 và f C Đ = 5
Mặt khác, ta có f(-4) = f(4) = 3
Vậy 
d) f(x) = | x 2 − 3x + 2| trên đoạn [-10; 10]
Khảo sát sự biến thiên và vẽ đồ thị của hàm số g(x) = x 2 – 3x + 2.
Ta có:
g′(x) = 2x − 3; g′(x) = 0 ⇔ x = 3/2
Bảng biến thiên:
Vì
nên ta có đồ thị f(x) như sau:
Từ đồ thị suy ra: min f(x) = f(1) = f(2) = 0; max = f(x) = f(−10) = 132
e) 
f′(x) < 0 nên và f’(x) > 0 trên (π/2; 5π/6] nên hàm số đạt cực tiểu tại x = π/2 và f C T = f(π/2) = 1
Mặt khác, f(π/3) = 2√3, f(5π/6) = 2
Vậy min f(x) = 1; max f(x) = 2
g) f(x) = 2sinx + sin2x trên đoạn [0; 3π/2]
f′(x) = 2cosx + 2cos2x = 4cos(x/2).cos3(x/2)
f′(x) = 0
⇔ 
Ta có: f(0) = 0,
Từ đó ta có: min f(x) = −2 ; max f(x) = 3√3/2
NV
Nguyễn Việt Lâm
Giáo viên
7 tháng 11 2019
a/ \(cosx>0\Rightarrow cosx=\sqrt{1-sin^2x}=\frac{4}{5}\)
\(\Rightarrow tanx=-\frac{3}{4}\Rightarrow A=\frac{129}{20}\)
b/ \(B=\frac{5sinx+3cosx}{3cosx-2sinx}=\frac{\frac{5sinx}{sinx}+\frac{3cosx}{sinx}}{\frac{3cosx}{sinx}-\frac{2sinx}{sinx}}=\frac{5+3cotx}{3cotx-2}=\frac{5+9}{9-2}\)
c/ \(C=\frac{sinx.cosx\left(cotx-2tanx\right)}{sinx.cosx\left(5cotx+tanx\right)}=\frac{cos^2x-2sin^2x}{5cos^2x+sin^2x}=\frac{cos^2x-2\left(1-cos^2x\right)}{5cos^2x+1-cos^2x}=\frac{3cos^2x-2}{4cos^2x+1}=...\)
d/ Không dịch được đề, ko biết mẫu số bên trái nó đến đâu cả
11 tháng 8 2020
Có thể giải giúp mình 5 câu trc 5 câu này đc k?? Do mk lm r mà k bk chắc đúng k nên ms hỏi vs nhìu khi đáp án sai nx
\(x\in\left(\dfrac{5}{2}\Omega;3\Omega\right)\)
=>\(x\in\left(\dfrac{\Omega}{2};\Omega\right)\)
=>\(cosx< 0\)
=>\(cosx=-\sqrt{1-\left(\dfrac{5}{8}\right)^2}=-\sqrt{1-\dfrac{25}{64}}=-\sqrt{\dfrac{39}{64}}=-\dfrac{\sqrt{39}}{8}\)
\(sin\left(x+\dfrac{\Omega}{3}\right)\)
\(=sinx\cdot cos\left(\dfrac{\Omega}{3}\right)+cosx\cdot sin\left(\dfrac{\Omega}{3}\right)\)
\(=\dfrac{5}{8}\cdot\dfrac{1}{2}+\dfrac{-\sqrt{39}}{8}\cdot\dfrac{\sqrt{3}}{2}=\dfrac{5-\sqrt{117}}{16}\)
Sinx =0,01827602763