Cho ΔABC vuông tại A (AB < AC). Gọi E là trung điểm BC. Trên tia AE lấy điểm D sao cho E là trung điểm của AD.a) Chứng minh: Tứ giác ABDC là hình chữ nhật.b) Trên tia CA lấy điểm K sao cho A là trung điểm của CK. Gọi F là trung điểm BK. Chứng minh: Tứ giác ACEF là hình bình hành.c) Từ D vẽ đường thẳng vuông góc với BC tại H, tia DH cắt đường thẳng FA tại I. Chứng minh: Tứ giác FIEB là hình thang cân.d)...
Đọc tiếp
Cho ΔABC vuông tại A (AB < AC). Gọi E là trung điểm BC. Trên tia AE lấy điểm D sao cho E là trung điểm của AD.
a) Chứng minh: Tứ giác ABDC là hình chữ nhật.
b) Trên tia CA lấy điểm K sao cho A là trung điểm của CK. Gọi F là trung điểm BK. Chứng minh: Tứ giác ACEF là hình bình hành.
c) Từ D vẽ đường thẳng vuông góc với BC tại H, tia DH cắt đường thẳng FA tại I. Chứng minh: Tứ giác FIEB là hình thang cân.
d) Chứng minh góc FIB = góc CDI.
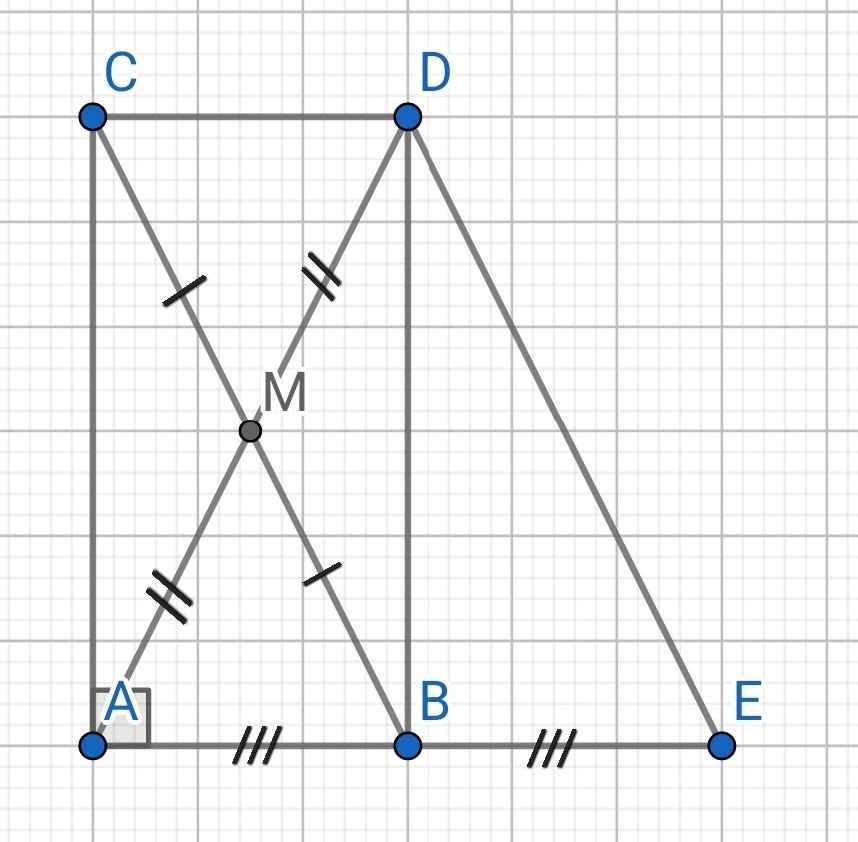
(Hình Tự vẽ)
Vì tam giác ABC có \(\widehat{A}=90\)
Mà AE là đường trung tuyến ( Vì E là trung điểm BC )
nên AE là đường trung tuyến ứng với cạnh huyễn
Suy ra \(AE=\frac{BC}{2}\)
hay AE = BE=EC (1)
Mà AE=ED (2)
Từ (1), và (2) suy ra AE=EB=EC=ED
Vì tứ giác ABDC có các đường chéo cắt nhau tại trung điểm mỗi đường và chúng đều bằng nhau
nên ABCD là hình chữ nhật
b, Vì EB=EC;FB=FK
nên EF là đường trung bình tam giác KBC
Suy ra EF//AC (1)
và EF=KC/2=AK=AC(2)
Từ (1) và (2) suy ra EF//AC VÀ EF=AC
Vậy ACEF là hình bình hành