Thực hịn phép tính :
5( 3xn+1 - yn-1 ) - 3( xn+1 + 2yn-1 ) + 4(-xn+1 + 2yn-1 )
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
12 tháng 7 2023
\(=-x^2y^3\cdot2x^{n-2}y^n+x^2y^3\cdot3x^ny^{n-3}-x^2y^3\cdot x^{n-2}y^{n-3}\)
\(=-2x^ny^{n+3}+3x^{n+2}y^n-x^ny^n\)
TN
0
CM
2 tháng 9 2019
Chọn A.
Ta có: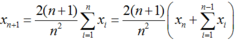 
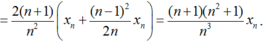
Do đó: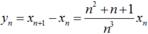 
- Ta chứng minh dãy (yn) tăng.
Ta có: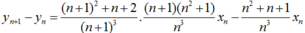 
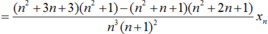
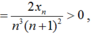
- Ta chứng minh dãy (yn) bị chặn.
Trước hết ta chứng minh: xn ≤ 4(n – 1) (1)
* Với n = 2, ta có: x2 = 4x1 = 4 nên (1) đúng với n = 2
* Giả sử (1) đúng với n, tức là: xn ≤ 4(n – 1), ta có
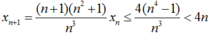
Nên (1) đúng với n + 1. Theo nguyên lí quy nạp ta suy ra (1) đúng
Ta có: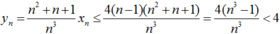 
Vậy bài toán được chứng minh.
27 tháng 6 2019
xn - 1(x + y) - y(xn - 1 + yn - 1)
= xn - x + y - yxn - y2 n - 1
5( 3xn+1 - yn-1 ) - 3( xn+1 + 2yn-1 ) + 4( -xn+1 + 2yn-1 )
= 15xn+1 - 5yn-1 - 3xn+1 - 6yn-1 - 4xn+1 + 8yn-1
= 8xn+1 - 3yn-1