Từ định nghĩa tích vô hướng \(\overrightarrow{u}.\overrightarrow{v}=u.v.cos\left(\overrightarrow{u};\overrightarrow{v}\right)\)chứng minh \(\overrightarrow{u}\left(a;b\right)\),\(\overrightarrow{v}\left(m;n\right)\)=(a.m;b.n)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HQ
Hà Quang Minh
Giáo viên
24 tháng 9 2023
Ta có: \(\overrightarrow u = \left( {0; - 5} \right),\;\overrightarrow v = \left( {\sqrt 3 ;1} \right)\)
\( \Rightarrow \overrightarrow u .\;\,\overrightarrow v = 0.\sqrt 3 + \left( { - 5} \right).1 = - 5.\)
HQ
Hà Quang Minh
Giáo viên
25 tháng 8 2023
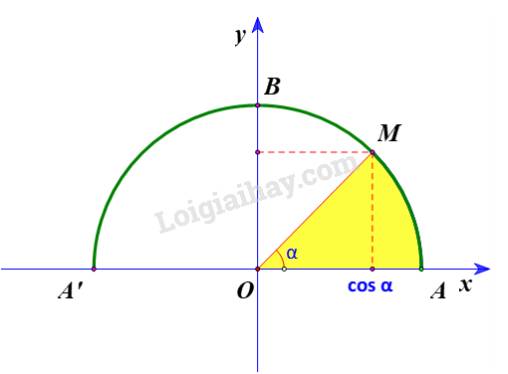
\(cos\left(\alpha-\beta\right)=x_M\cdot x_N=cos\alpha\cdot cos\beta+sin\alpha\cdot sin\beta\\ cos\left(\alpha+\beta\right)=cos\left[\alpha-\left(-\beta\right)\right]=cos\alpha\cdot cos\left(-\beta\right)+sin\alpha\cdot sin\left(-\beta\right)=cos\alpha\cdot cos\beta-sin\alpha\cdot sin\beta\)
24 tháng 9 2023
Tham khảo:
Dễ thấy: \(\overrightarrow u .\;\overrightarrow v \) cùng dấu với \(\cos \;\left( {\overrightarrow u ,\;\overrightarrow v } \right)\) (do \(\left| {\overrightarrow u } \right|.\;\left| {\overrightarrow v } \right| > 0\)). Do đó:
+) \(\overrightarrow u .\;\overrightarrow v \;\; > 0\) \( \Leftrightarrow \cos \;\left( {\overrightarrow u ,\;\overrightarrow v } \right) > 0\) hay \({0^o} \le \left( {\overrightarrow u ,\;\overrightarrow v } \right) < {90^o}\)
+) \(\overrightarrow u .\;\overrightarrow v \;\; < 0\) \( \Leftrightarrow \cos \;\left( {\overrightarrow u ,\;\overrightarrow v } \right)\;\; < 0\) hay \({90^o} < \left( {\overrightarrow u ,\;\overrightarrow v } \right) \le {180^o}\)
Vậy \(\overrightarrow u .\;\overrightarrow v \;\; > 0\) nếu \({0^o} \le \left( {\overrightarrow u ,\;\overrightarrow v } \right) < {90^o}\) và \(\overrightarrow u .\;\overrightarrow v \;\; < 0\) nếu \({90^o} < \left( {\overrightarrow u ,\;\overrightarrow v } \right) \le {180^o}.\)
HQ
Hà Quang Minh
Giáo viên
24 tháng 9 2023
a)
Ta có: \(\overrightarrow u .\;\overrightarrow v = \left| {\overrightarrow u } \right|.\;\left| {\overrightarrow v } \right|.\cos \left( {\overrightarrow u ,\;\overrightarrow v } \right) = \left| {\overrightarrow u } \right|.\;\left| {\overrightarrow v } \right|\)
\( \Rightarrow \cos \left( {\overrightarrow u ,\;\overrightarrow v } \right) = 1 \Leftrightarrow \left( {\overrightarrow u ,\;\overrightarrow v } \right) = {0^o}\)
Nói cách khác: \(\overrightarrow u ,\;\overrightarrow v \) cùng hướng.
b)
Ta có: \(\overrightarrow u .\;\overrightarrow v = \left| {\overrightarrow u } \right|.\;\left| {\overrightarrow v } \right|.\cos \left( {\overrightarrow u ,\;\overrightarrow v } \right) =- \left| {\overrightarrow u } \right|.\;\left| {\overrightarrow v } \right|\)
\( \Rightarrow \cos \left( {\overrightarrow u ,\;\overrightarrow v } \right) = - 1 \Leftrightarrow \left( {\overrightarrow u ,\;\overrightarrow v } \right) = {180^o}\)
Nói cách khác: \(\overrightarrow u ,\;\overrightarrow v \) ngược hướng.
24 tháng 9 2023
Tham khảo:
Kí hiệu O, E, F là các điểm như trên hình vẽ.
Dễ thấy: tứ giác OEMF là hình bình hành nên \(\overrightarrow {OE} + \overrightarrow {OF} = \overrightarrow {OM} \) hay \(\overrightarrow v + \overrightarrow u = \overrightarrow {OM} \)
Và \(\overrightarrow {OC} = 3.\overrightarrow {OM} \Rightarrow 3\left( {\overrightarrow v + \overrightarrow u } \right) = 3.\overrightarrow {OM} = \overrightarrow {OC} \)
Mặt khác: \(\overrightarrow {OA} = 3.\overrightarrow {OF} = 3\;\overrightarrow u ;\;\overrightarrow {OB} = 3.\overrightarrow {OE} = 3\;\overrightarrow v \)
Và \(\overrightarrow {OB} + \overrightarrow {OA} = \overrightarrow {OC} \) hay \(3\;\overrightarrow v + 3\;\overrightarrow u = \overrightarrow {OC} \)
\( \Rightarrow 3\left( {\overrightarrow v + \overrightarrow u } \right) = 3\;\overrightarrow v + 3\;\overrightarrow u \)
20 tháng 12 2022
a: AB=BC=CD=DA=6a
\(AC=BD=\sqrt{\left(6a\right)^2+\left(6a\right)^2}=6a\sqrt{2}\)
\(\left|\overrightarrow{AB}-\overrightarrow{AC}\right|=\left|\overrightarrow{CA}+\overrightarrow{AB}\right|=CB=6a\)
\(\left|\overrightarrow{BC}+\overrightarrow{BD}\right|=\sqrt{BC^2+BD^2+2\cdot BC\cdot BD\cdot cos45}\)
\(=\sqrt{36a^2+72a^2+\sqrt{2}\cdot6a\cdot6a\sqrt{2}}\)
\(=6a\sqrt{5}\)
b: \(\overrightarrow{AB}\cdot\overrightarrow{AC}=AB\cdot AC\cdot cos\left(\overrightarrow{AB},\overrightarrow{AC}\right)=6a\cdot6a\sqrt{2}\cdot\dfrac{\sqrt{2}}{2}\)
\(=36a^2\)