41.cho △ ABC,các đg trung tuyến AD,BE,CF.ĐG thẳng kẻ qua E song song với AB,qua F song song với BE cắt nhau ở G.CM:
a) tứ giác AFEG là hình bình hành
b) 3 điểm D,E,G thẳng hàng và CG=AD
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lời giải:
a. $M,N$ đối xứng nhau qua $O$ nghĩa là $O$ là trung điểm $MN$
Tứ giác $AMBN$ có 2 đường chéo $AB, MN$ cắt nhau tại trung điểm $O$ của mỗi đường nên $AMBN$ là hbh $(1)$
Mặt khác, tam giác $ABC$ cân tại $A$ nên trung tuyến $AM$ đồng thời là đường cao
$\Rightarrow AM\perp BC$ nên $\widehat{AMB}=90^0(2)$
Từ $(1); (2)\Rightarrow AMBN$ là hình chữ nhật
b. Vì $AMBN$ là hcn nên $BM\parallel AN$ và $BM=AN$
Mà $B,M,C$ thẳng hàng và $BM=MC$ nên:
$AN\parallel CM, AN=CM$
$\Rightarrow ACMN$ là hình bình hành
c.
$ACMN$ là hbh nên $MN\parallel AC$
Để $ACMN$ là hình vuông thì $MN\perp AB$
$\Leftrightarrow AC\perp AB$
$\Leftrightarrow ABC$ là tam giác vuông tại $A$

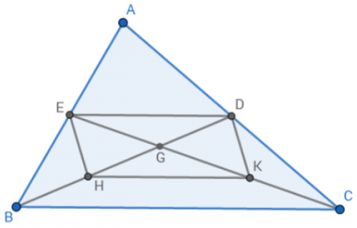
a)
BD là đường trung tuyến của Δ ABC nên D là trung điểm của AC (1)
CE là đường trung tuyến của Δ ABC nên E là trung điểm của AB (2)
Từ (1) và (2) suy ra :
DE là đường trung bình của Δ ABC
=> DE // BC và DE = 1/2 BC
Δ BGC có H là trung điểm của GB và K là trung điểm của GC
suy ra HK là đường trung bình của Δ BGC
=> HK // BC và HK = 1/2 BC
Tứ giác DEHK có DE//BC, HK // BC và DE = HK = 1/2 BC
nên tứ giác
b) DEHK là hình bình hành nên
HG = GD = 1/2 HD và GE = GK = 1/2 EK
Để tứ giác DEHK là hình chữ nhật thì
HD = EK => 1/2 HD = 1/2 EK => GE = GD và GH = GK
GH = GK => 2GH = 2GK => GB = GC
Xét Δ GEB và Δ GDC có
GE = GD Góc EGB = góc DGC GB = GC => ΔGEB = ΔGDC (c.g.c) => BE = CD => 2BE = 2CD => AB = AC => ΔABC cân tại A Vậy đểtứ giác DEHK là hình chữ nhật thì
ΔABC cân tại Ac) BD ⊥ CE => HD ⊥ EK Hình bình hành DEHK có HD ⊥ EK nên DEHK là hình thoi Vậy
nếu các đường trung tuyến BD và CE vuông góc với nhau thì tứ giác DEHK là hình thoi

a, Xét tứ giác AMCK có :
AI=IC (gt)
MI=IK
=> AMCK la HBH
Mà AM là trung tuyến của tam giác ABC
=> AM cũng là đường cao của tam giác ABC
Nên hinh binh hanh AKCM có 1 góc vuông là M=90
=> AKCM là hình chữ nhật
b, Xét tứ giác AKMB co :
AK=MC (tính chất hình chữ nhật AKMC)
Mà BM=MC =>AK=BM (1)
Va AK//MC=>AK//MC (2)
Từ (1)(2) suy ra AKMB là hình bình hành
c, Tam giác ABC phai là tam giác vuông và vuông tại B để tứ giác AKMB là hình thoi
a: Xét tứ giác BFGE có
BF//GE
BE//FG
Do đó: BFGE là hình bình hành
=>GE//BF và GE=BF
ta có: GE//BF
F\(\in\)BA
Do đó: GE//AB và GE//AF
Ta có: GE=BF
BF=AF
Do đó: GE=AF
Xét tứ giác AFEG có
AF//GE
AF=GE
Do đó: AFEG là hình bình hành
b: Xét ΔCAB có
D,E lần lượt là trung điểm của CB,CA
=>DE là đường trung bình của ΔCAB
=>DE//AB và \(DE=\dfrac{AB}{2}=FB=FA\)
Ta có: DE//AB
EG//AB
mà DE,EG có điểm chung là E
nên D,E,G thẳng hàng
Ta có: DE=FB
GE=FB
Do đó: DE=EG
mà D,E,G thẳng hàng
nên E là trung điểm của DG
Ta có: DG=2DE
AB=2FB
mà DE=FB
nên DG=AB
Xét tứ giác AGBD có
AB//DG
AB=DG
Do đó: AGBD là hình bình hành
=>AG//BD và AG=BD
Ta có: AG//BD
D thuộc BC
Do đó: AG//DC
Ta có: AG=BD
BD=DC
Do đó: AG=CD
Xét tứ giác AGCD có
AG//CD
AG=CD
Do đó: AGCD là hình bình hành
=>CG=AD