2. rút gọn các bthuc
a) 2\(\sqrt{27}\) - 3\(\sqrt{54}\) - \(\dfrac{1}{3}\)\(\sqrt{48}\)
b) \(\dfrac{-1}{2}\)\(\sqrt{108}\) + \(\dfrac{1}{15}\)\(\sqrt{75}\) - \(\dfrac{1}{3}\)\(\sqrt{363}\)
c) \(\dfrac{5}{8}\)\(\sqrt{48}\) - \(\dfrac{1}{33}\)\(\sqrt{363}\) + \(\dfrac{3}{14}\)\(\sqrt{147}\)
d)\(\dfrac{x-9}{x-9\sqrt{ }x}\) - \(\dfrac{x-4}{\sqrt{x}+2}\)
e) \(\dfrac{x+2\sqrt{x}+1}{\sqrt{x}+1}\) - \(\dfrac{x-4\sqrt{x}+4}{\sqrt{x}-2}\)

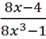
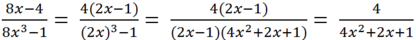
a: \(2\sqrt{27}-3\sqrt{54}-\dfrac{1}{3}\sqrt{48}\)
\(=2\cdot3\sqrt{3}-3\cdot3\sqrt{6}-\dfrac{1}{3}\cdot4\sqrt{3}\)
\(=6\sqrt{3}-9\sqrt{6}-\dfrac{4}{3}\sqrt{3}=\dfrac{14}{3}\sqrt[]{3}-9\sqrt{6}\)
b: \(-\dfrac{1}{2}\sqrt{108}+\dfrac{1}{15}\cdot\sqrt{75}-\dfrac{1}{3}\cdot\sqrt{363}\)
\(=-\dfrac{1}{2}\cdot6\sqrt{3}+\dfrac{1}{15}\cdot5\sqrt{3}-\dfrac{1}{3}\cdot11\sqrt{3}\)
\(=-3\sqrt{3}+\dfrac{1}{3}\sqrt{3}-\dfrac{11}{3}\sqrt{3}=-\dfrac{19}{3}\sqrt{3}\)
c: \(\dfrac{5}{8}\sqrt{48}-\dfrac{1}{33}\cdot\sqrt{363}+\dfrac{3}{14}\cdot\sqrt{147}\)
\(=\dfrac{5}{8}\cdot4\sqrt{3}-\dfrac{1}{33}\cdot11\sqrt{3}+\dfrac{3}{14}\cdot7\sqrt{3}\)
\(=\dfrac{5}{2}\sqrt{3}-\dfrac{1}{3}\sqrt{3}+\dfrac{3}{2}\sqrt{3}=\dfrac{11}{3}\sqrt{3}\)
d:
ĐKXĐ: x>=0; x<>9
Sửa đề:\(\dfrac{x-9}{x-3\sqrt{x}}-\dfrac{x-4}{\sqrt{x}+2}\)
\(=\dfrac{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}{\sqrt{x}\left(\sqrt{x}-3\right)}-\dfrac{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}{\sqrt{x}+2}\)
\(=\dfrac{\sqrt{x}+3}{\sqrt{x}}-\left(\sqrt{x}-2\right)=\dfrac{\sqrt{x}+3-x+2\sqrt{x}}{\sqrt{x}}\)
\(=\dfrac{-x+3\sqrt{x}+3}{\sqrt{x}}\)
e: ĐKXĐ: x>=0; x<>4
\(\dfrac{x+2\sqrt{x}+1}{\sqrt{x}+1}-\dfrac{x-4\sqrt{x}+4}{\sqrt{x}-2}\)
\(=\dfrac{\left(\sqrt{x}+1\right)^2}{\sqrt{x}+1}-\dfrac{\left(\sqrt{x}-2\right)^2}{\sqrt{x}-2}\)
\(=\sqrt{x}+1-\sqrt{x}+2=3\)