Chứng minh rằng 21+22+23+24+...+2108 chia hết cho 7
Giúp mình giải nhe
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(A+2+2^2+2^3+...+2^{100}\)
\(=\left(2+2^2\right)+2^2\left(2+2^2\right)+...+2^{98}\left(2+2^2\right)\)
\(=6+2^2.6+...+2^{98}.6=6\left(1+2^2+...+2^{98}\right)⋮6\)
\(A=2+2^2+2^3+2^4+...+2^{100}\)
\(=2\cdot3+...+2^{99}\cdot3\)
\(=6\left(1+...+2^{99}\right)⋮6\)

Ta có :
\(A=2+2^2+2^3+2^4...2^{2010}\)\(^0\)
\(=2\left(1+2\right)+2^3\left(1+2\right)+...+2^{2009}\left(1+2\right)\)
\(=2.3+2^3.3+....+2^{2009}.3\)
\(=3\left(2+2^3+....+2^{2009}\right)⋮3\)
Ta có :
\(2+2^2+2^3+2^4+....+2^{2010}\)
\(=2\left(1+2+2^2\right)+2^4\left(1+2+2^2\right)+...+2^{2008}\left(1+2+2^2\right)\)
\(=2.7+2^4.7+....+2^{2008}.7\)
\(=7\left(2+2^4+....+2^{2008}\right)⋮7\)
Vậy \(2^1+2^2+2^3+2^4+...+2^{2010}⋮3\) và \(7\)

*Sửa lại đề*
A = 21+ 22+ 23+ 24 + .. + 2100
A = (21+22) + (23+ 24) +...+ (299+ 2100)
A = 2.(1+2) + 23.(1+2) + .. + 299. (1+2)
A = 2.3 + 23. 3 + .. + 299.3
A = 3 . (21 + 23 + .... + 299)
Mà 3 chia hết cho 3
=> A chia hết cho 3

c) \(55-7.\left(x+3\right)=6\)
\(7.\left(x+3\right)=55-6\)
\(7.\left(x+3\right)=49\)
\(x+3=49:7\)
\(x+3=7\)
\(x=7-3\)
\(x=4\)
d) \(-14-x+\left(-15\right)=-10\)
\(-29-x=-10\)
\(x=-29+10\)
\(x=-19\)
-----------------------------
Số số hạng của A:
\(60-1+1=60\) (số)
Do \(60⋮6\) nên ta có thể nhóm các số hạng của A thành từng nhóm mà mỗi nhóm có 6 số hạng như sau:
\(A=\left(2+2^2+2^3+2^4+2^5+2^6\right)+\left(2^7+2^8+2^9+2^{10}+2^{11}+2^{12}\right)+...+\left(2^{55}+2^{56}+2^{57}+2^{58}+2^{59}+2^{60}\right)\)
\(=2.\left(1+2+2^2+2^3+2^4+2^5\right)+2^7.\left(1+2+2^2+2^3+2^4+2^5\right)+...+2^{55}.\left(1+2+2^2+2^3+2^4+2^5\right)\)
\(=2.63+2^7.63+...+2^{55}.63\)
\(=63.\left(2+2^7+...+2^{55}\right)\)
\(=21.3.\left(2+2^7+...+2^{55}\right)⋮21\)
Vậy \(A⋮21\)
55-7(x+3)=6
7(x+3)=55-6=49
(x+3)=49:7=7
x=7-3=4
(-14)-x + (-15)=-10
(-14)-x=-10-15=-25
x =-14-25=-39
A chia hết 31 chứ

A=2(1+2)+2^3(1+2)+...+2^2009(1+2)
=3(2+2^3+...+2^2009) chia hết cho 3
A=2(1+2+2^2)+2^4(1+2+2^2)+...+2^2008(1+2+2^2)
=7(2+2^4+...+2^2008) chia hết cho 7

A = 20 + 21 + 22 + 23 + 24 + 25 … + 299
A=( 20 + 21 + 22 + 23 + 24) +( 25 … + 299)
A= 20.(20 + 21 + 22 + 23 + 24)+25.( 25 … + 299)
A= 1. 31+ 25.31… + 295.31
A= 31. (1+25...+295)
KL: ......
\(A=2^0+2^1+2^2+2^3+2^4+...+2^{99}=\left(2^0+2^1+2^2+2^3+2^4\right)+2^5\left(2^0+2^1+2^2+2^3+2^4\right)+...+2^{95}\left(2^0+2^1+2^2+2^3+2^4\right)=31+31.2^5+...+31.2^{95}=31\left(1+2^5+...+2^{95}\right)⋮31\)
Cho A = 1 + 2 + 22 + 23 + 24 +…299 Chứng minh rằng: A chia hết cho 3
Ghi cách làm và đáp án giúp mình

\(A=1+2+2^2+2^3+....+2^{98}+2^{99}\\ \Leftrightarrow A=\left(1+2\right)+\left(2^2+2^3\right)+\left(2^4+2^5\right)+....+\left(2^{98}+2^{99}\right)\\ \Leftrightarrow A=3+2^2.\left(1+2\right)+2^4.\left(1+2\right)+....+2^{98}.\left(1+2\right)\\ \Leftrightarrow A=3+3.2^2+3.2^4+....+3.2^{98}\\ \Leftrightarrow A=3.\left(1+2^2+2^4+...+2^{98}\right)⋮3\)

Câu 1:
$A=(2+2^2)+(2^3+2^4)+(2^5+2^6)+....+(2^{2019}+2^{2020})$
$=2(1+2)+2^3(1+2)+2^5(1+2)+....+2^{2019}(1+2)$
$=(1+2)(2+2^3+2^5+...+2^{2019})=3(2+2^3+2^5+...+2^{2019})\vdots 3$
-----------------
$A=2+(2^2+2^3+2^4)+(2^5+2^6+2^7)+....+(2^{2018}+2^{2019}+2^{2020})$
$=2+2^2(1+2+2^2)+2^5(1+2+2^2)+....+2^{2018}(1+2+2^2)$
$=2+(1+2+2^2)(2^2+2^5+....+2^{2018})$
$=2+7(2^2+2^5+...+2^{2018})$
$\Rightarrow A$ chia $7$ dư $2$.
Câu 2:
$B=(3+3^2)+(3^3+3^4)+....+(3^{2021}+3^{2022})$
$=3(1+3)+3^3(1+3)+...+3^{2021}(1+3)$
$=(1+3)(3+3^3+...+3^{2021})=4(3+3^3+....+3^{2021})\vdots 4$
-------------------
$B=(3+3^2+3^3)+(3^4+3^5+3^6)+...+(3^{2020}+3^{2021}+3^{2022})$
$=3(1+3+3^2)+3^4(1+3+3^2)+....+3^{2020}(1+3+3^2)$
$=(1+3+3^2)(3+3^4+...+3^{2020})=13(3+3^4+...+3^{2020})\vdots 13$ (đpcm)

Đề sai, viết lại thành:
A= 21+22+23+24+...+259+260
Giải:
A=21+22+23+...............+259+260
A=(21+22+23)+...............+(258+259+260)
A=2.(1+2+22)+............+258.(1+2+22)
A=2.7+.......................+258.7
A=(2+24+..............+258).7 ⋮ 7(đpcm)
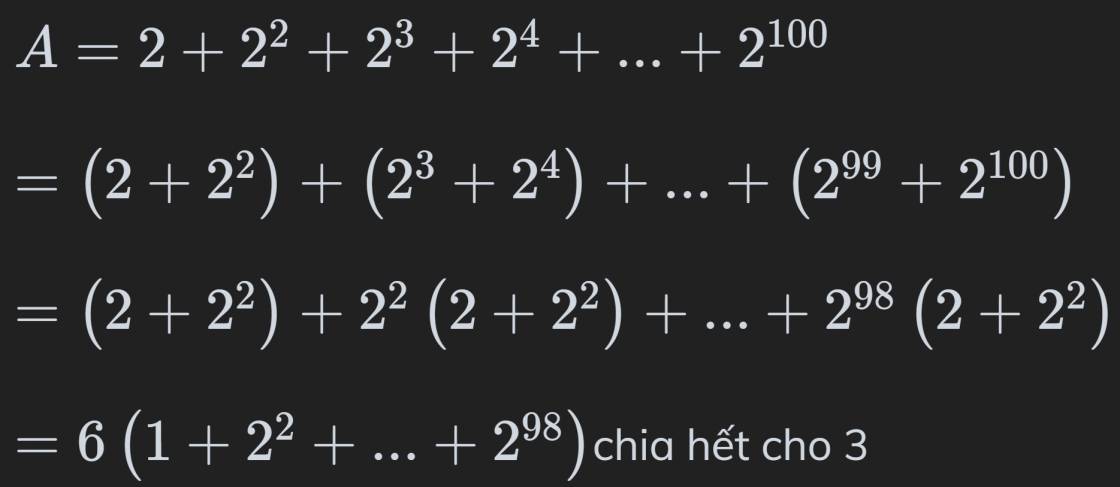
Đặt \(A=2^1+2^2+...+2^{108}\)
\(\Rightarrow2A=2^2+2^3+...+2^{109}\)
\(\Rightarrow A=2^{109}-2\)
Ta có \(A=2^{109}-2^{106}+2^{106}-2^{103}+2^{103}-2^{100}+...+2^4-2\)
\(=2^{106}\left(2^3-1\right)+2^{103}\left(2^3-1\right)+...+2\left(2^3-1\right)\)
\(=7\left(2^{106}+2^{103}+...+2\right)⋮7\)
Vậy A chia hết cho 7.
Ta có : 21+22+23+24+.....+2108=
=( 21+22+23 )+( 24+25+26 )+.....+( 2106+ 2107+2108 )
=21 ( 1+2+4 )+24 ( 1+2+4 )+.....+2106( 1+2+4 )
=21 .7+24 .7+....+2106. 7
=7 ( 21+24+......+2106 ) \(⋮\)7
Vậy 21+23+24+....+2108\(⋮\)7
\(⋮\)