Tìm n \(\in\)Z để 2n2 - n + 2 chia hết cho 2n + 1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
9 tháng 5 2017
Cách 1: Thực hiện phép chia 2n2 – n + 2 cho 2n + 1 ta có:
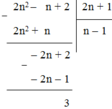
2n2 – n + 2 chia hết cho 2n + 1
⇔ 3 ⋮ (2n + 1) hay (2n + 1) ∈ Ư(3)
⇔ 2n + 1 ∈ {±1; ±3}
+ 2n + 1 = 1 ⇔ 2n = 0 ⇔ n = 0
+ 2n + 1 = -1 ⇔ 2n = -2 ⇔ n = -1
+ 2n + 1 = 3 ⇔ 2n = 2 ⇔ n = 1
+ 2n + 1 = -3 ⇔ 2n = -4 ⇔ n = -2.
Vậy n ∈ {-2; -1; 0; 1.}
Cách 2:
Ta có:
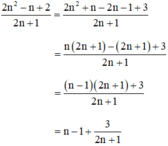
2n2 – n + 2 chia hết cho 2n + 1
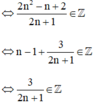
⇔ 2n + 1 ∈ Ư(3) = {±1; ± 3}.
+ 2n + 1 = 1 ⇔ 2n = 0 ⇔ n = 0
+ 2n + 1 = -1 ⇔ 2n = -2 ⇔ n = -1
+ 2n + 1 = 3 ⇔ 2n = 2 ⇔ n = 1
+ 2n + 1 = -3 ⇔ 2n = -4 ⇔ n = -2.
Vậy n ∈ {-2; -1; 0; 1.}
Chú ý: Đa thức A chia hết cho đa thức B khi phần dư của phép chia bằng 0.
DF
1
HH
2 tháng 7 2020
Thực hiện phép chia 2n2 – n + 2 cho 2n + 1 ta có:
2n2 – n + 2 chia hết cho 2n + 1
<=> 3 \(⋮\)( 2n + 1 ) hay ( 2n + 1 ) \(\in\) Ư(3)
<=> 2n + 1 \(\in\) {\(\pm\)1; \(\pm\)3 }
+ 2n + 1 = 1 <=> 2n = 0 <=> n = 0
+ 2n + 1 = -1 <=> 2n = -2 <=> n = -1
+ 2n + 1 = 3 <=> 2n = 2 <=> n = 1
+ 2n + 1 = -3 <=> 2n = -4 <=> n = -2.
Vậy n \(\in\) { -2 ; -1 ; 0 ; 1 }
AH
Akai Haruma
Giáo viên
10 tháng 12 2023
Bài 1:
\(=-5^{22}+222+[-122-(100-5^{22})+2022]\)
\(=-5^{22}+222-122-100+5^{22}+2022\\ =(-5^{22}+5^{22})+(222-122-100)+2022\\ =0+0+2022=2022\)
AH
Akai Haruma
Giáo viên
10 tháng 12 2023
Bài 2:
$2n^2+n-6\vdots 2n+1$
$\Rightarrow n(2n+1)-6\vdots 2n+1$
$\Rightarrow 6\vdots 2n+1$
$\Rightarrow 2n+1\in Ư(6)$
Mà $2n+1$ lẻ nên $2n+1\in \left\{\pm 1; \pm 3\right\}$
$\Rightarrow n\in \left\{0; -1; 1; -2\right\}$
3 tháng 7 2023
1:
2n^2+5n-1 chia hết cho 2n-1
=>2n^2-n+6n-3+2 chia hết cho 2n-1
=>2n-1 thuộc {1;-1;2;-2}
mà n nguyên
nên n=1 hoặc n=0
2:
a: A=n(n+1)(n+2)
Vì n;n+1;n+2 là 3 số liên tiếp
nên A=n(n+1)(n+2) chia hết cho 3!=6
b: B=(2n-1)[(2n-1)^2-1]
=(2n-1)(2n-2)*2n
=4n(n-1)(2n-1)
Vì n;n-1 là hai số nguyên liên tiếp
nên n(n-1) chia hết cho 2
=>B chia hết cho 8
c: C=n^2+14n+49-n^2+10n-25=24n+24=24(n+1) chia hết cho 24
16 tháng 7 2018
Ta có: \(\frac{2n^2-n+2}{2n+1}=\frac{2n^2+n-2n-1+3}{2n+1}=\frac{n\left(2n+1\right)-\left(2n+1\right)+3}{2n+1}=\frac{\left(2n+1\right)\left(n-1\right)+3}{2n+1}\)
Vì (2n+1) chia hết cho 2n+1 => (2n+1)(n-1) chia hết cho 2n+1
Nên để 2n2 - n + 2 chia hết cho 2n + 1 thì 3 phải chia hết cho 2n+1
=> \(2n+1\inƯ\left(3\right)=\left\{-1;1;3;-3\right\}\)
Nếu 2n + 1 = 1 thì n = 0 (thỏa mãn x thuộc Z)
Nếu 2n + 1 = -1 thì n = -1 (thỏa mãn x thuộc Z)
Nếu 2n + 1 = 3 thì n = 1 (thỏa mãn x thuộc Z)
Nếu 2n + 1 = -3 thì n = -2 (thỏa mãn x thuộc Z)
Vậy để 2n2 - n + 2 chia hết cho 2n + 1 <=> n = {0;-1;-2;1}
16 tháng 7 2018
ta có: 2n2 - n + 2 chia hết cho 2n + 1
=> 2n2 + n - 2n + 2 chia hết cho 2n + 1
n.(2n+1) - ( 2n + 1) + 3 chia hết cho 2n + 1
(2n+1).(n-1) + 3 chia hết cho 2n + 1
mà (2n+1).(n-1) chia hết cho 2n + 1
=> 3 chia hết cho 2n + 1
=>...
AH
Akai Haruma
Giáo viên
2 tháng 1
1/
$10n+4\vdots 2n+7$
$\Rightarrow 5(2n+7)-31\vdots 2n+7$
$\Rightarrow 31\vdots 2n+7$
$\Rightarrow 2n+7\in Ư(31)$
$\Rightarrow 2n+7\in \left\{1; -1; 31; -31\right\}$
$\Rightarrow n\in \left\{-3; -4; 12; -19\right\}$
AH
Akai Haruma
Giáo viên
2 tháng 1
2/
$5n-4\vdots 3n+1$
$\Rightarrow 3(5n-4)\vdots 3n+1$
$\Rightarroq 15n-12\vdots 3n+1$
$\Rightarrow 5(3n+1)-17\vdots 3n+1$
$\Rightarrow 17\vdots 3n+1$
$\Rightarrow 3n+1\in Ư(17)$
$\Rightarrow 3n+1\in \left\{1; -1; 17; -17\right\}$
$\Rightarrow n\in \left\{0; \frac{-2}{3}; \frac{16}{3}; -6\right\}$
Do $n$ nguyên nên $n\in\left\{0; -6\right\}$
5 tháng 2 2022
a: \(\Leftrightarrow2n^2+n-2n-1+3⋮2n+1\)
\(\Leftrightarrow2n+1\in\left\{1;-1;3;-3\right\}\)
hay \(n\in\left\{0;-1;1;-2\right\}\)
b: \(\Leftrightarrow2n^2-4n+5n-10+3⋮n-2\)
\(\Leftrightarrow n-2\in\left\{1;-1;3;-3\right\}\)
hay \(n\in\left\{3;1;5;-1\right\}\)
c: \(\Leftrightarrow10n^2-15n+8n-12+7⋮2n-3\)
\(\Leftrightarrow2n-3\in\left\{1;-1;7;-7\right\}\)
hay \(n\in\left\{2;1;5;-2\right\}\)
d: \(\Leftrightarrow2n^2-n+4n-2+5⋮2n-1\)
\(\Leftrightarrow2n-1\in\left\{1;-1;5;-5\right\}\)
hay \(n\in\left\{1;0;3;-2\right\}\)
2n² - n + 2. │ 2n + 1
2n² + n....... ├------------
------------------ I n - 1
.......-2n + 2
.......-2n - 1
_____________
3
Để chia hết thì: 3 phai chia hết cho ( 2n + 1)
hay (2n + 1) la ước của 3
Ư(3) = {±1 ; ±3}
______________________________
+) 2n + 1 = 1 <=> n = 0
+) 2n + 1 = -1 <=> n = -1
+) 2n + 1 = 3 <=> n = 1
+) 2n + 1 = -3 <=> n = -2
Vậy n ∈{0;-2 ; ±1}
Ta có: 2n2 – n + 2 : (2n + 1)
2015-10-01_000139
Ta có: n ∈ Z và 2n2 – n + 2 chia hết cho 2n +1 thì 2n + 1 là ước của 3. Ước của 3 là ±1; ± 3
Khi 2n + 1 = 1 ⇔2n = 0 ⇔ n = 0
Khi 2n + 1 = -1 ⇔ 2n = -2 ⇔ n = -1
Khi 2n + 1 = 3 ⇔ 2n = 2 ⇔ n – 1
Khi 2n + 1 = -3 ⇔ 2n = -4 ⇔ n = -2
Vậy, n = 0 hoặc n = – 1 hoặc n = 1 hoặc n = -2.