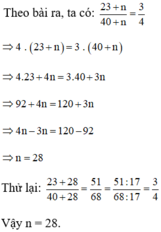Cộng cả tử và mẫu của phân số 12/17 với cùng 1 số tự nhiên x rồi rút gọn được 4/5. Tìm x
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
HV
Hoàng văn Đức
23 tháng 2 2021
Ta có:
12+x/17+x=4/5
(12+x).5=17+x.4
60+5x=68+4x
5x-4x=68-60
x=8
Đúng(0)
Những câu hỏi liên quan
DD
Đoàn Đức Hà
Giáo viên
1 tháng 8 2021
Khi cộng cả tử và mẫu của phân số đã cho với một số \(x\)thì hiệu tử số và mẫu số không đổi.
Hiệu tử số và mẫu số là:
\(17-12=5\)
Nếu phân số mới có tử là \(4\)phần thì mẫu là \(5\)phần.
Hiệu số phần bằng nhau là:
\(5-4=1\)(phần)
Tử số phân số mới là:
\(5\div1\times4=20\)
\(x\)bằng:
\(20-12=8\)
AH
Akai Haruma
Giáo viên
30 tháng 7
Lời giải:
Ta có:
$\frac{12+x}{17+x}=\frac{4}{5}$
$\Rightarrow 5(x+12)=4(x+17)$
$\Rightarrow 5x+60=4x+68$
$\Rightarrow x=8$
L
2
15 tháng 2 2016
Cộng cả tử và mẫu của phân số 23/40 với cùng một số tự nhiên n rồi rút gọn, ta được 3/4. Tìm n
theo bài ra ta có: \(\frac{23+n}{40+n}=\frac{3}{4}=>\left(23+n\right)\cdot4=\left(40+n\right)\cdot3=>92+4n=120+3n=>4n-3n=120-92=>n=28\)
12 tháng 3 2018
Từ đề bài ta có :
\(\frac{13+n}{29+n}=\frac{5}{9}\)
\(\Rightarrow9\left(13+n\right)=5\left(29+n\right)\)
\(\Rightarrow117+9n=145+5n\)
\(\Rightarrow9n-5n=145-117\)
\(\Rightarrow4n=28\)
\(\Rightarrow n=7\)
Vậy n = 7
Thử lại : \(\frac{13+n}{29+n}=\frac{13+7}{29+7}=\frac{20}{36}=\frac{5}{9}\)(đúng)
10 tháng 5 2020
Bài giải :
Hiệu mẫu số và tử số là :
23 - 15 = 8
Tử số mới là :
8 : ( 3 - 2 ) . 2 = 16
Số n là :
16 - 15 = 1
Vậy n = ...
#hoctot
#Ako_oml
21 tháng 2 2016
23+n40+n=34
Mà 40+n−(23+n)=17
Áp dụng "Tìm 2 số khi biết hiệu và tỉ của 2 số đó" để tìm 23+n sau đó tìm được n
TV
1
HP
17 tháng 2 2016
theo bài ra ta có:
\(\frac{23+n}{40+n}=\frac{3}{4}\)
=>(23+n).4=(40+n).3
=>92+4n=120+3n
=>4n-3n=120-92
=>n=28
vậy n=28
HN
10
HP
3 tháng 2 2016
Theo bài ra ta có:
\(\frac{23+n}{40+n}=\frac{3}{4}\)
=>(23+n).4=(40+n).3 (nhân chéo)
=>92+4n=120+3n
=>4n-3n=120-92
=>n=28
Vậy cần thêm n=28 thì 23+n/40+n=3/4
tick nhé
*. là "x"
LM
3 tháng 2 2016
Bài giải
Theo đề bài, ta có:
\(\frac{23+n}{40+n}=\frac{3}{4}\)
Ta thấy hai số tự nhiên (23 và 40) khác nhau mà đều cộng cùng một số tự nhiên n thì hiệu của hai số tự nhiên đó vẫn không thay đổi. Vậy, hiệu giữa hai số tự nhiên 23 và 40 là:
40 - 23 = 17
Ta có sơ đồ sau:
Tử số : |----------|----------|----------| 17
Mẫu số : |----------|----------|----------|----------|
Hiệu số phân tương ứng với 17 là:
4 - 3 = 1 (phần)
Tử số của phân số \(\frac{23}{40}\) sau khi thay đổi là:
17 : 1 . 3 = 51
Số tự nhiên n cần tìm là:
51 - 23 = 28
Vậy, n = 28
CM
4 tháng 1 2019
Sau khi cộng cả tử và mẫu của phân số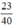 
với cùng một số tự nhiên n, ta được phân số mới là 
.
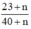