 Helpppp meeeee!!!!!!!!!!
Helpppp meeeee!!!!!!!!!!
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Gọi tứ giác nằm ngang là ABCD.
Hình dựng đứng là ABEMN
Từ điểm M kẻ đường thẳng//AB cắt BE tại G.
Do NM_|_AN tại A
MN//AB; BG//AN
=>BG_|_BE nên tam giác MGE vuông tại G. (1)
=>Tứ giác ABGN là hình chữ nhật=Hình chữ nhật ABCD( vì AB//=CD=14,2 m)
=>AN=AC=5 (m)
Từ (1) =>EG là đường cao của tam giác MGE có cạnh đáy MG.
=>EG=BE-BG=8-5=3 (m)
=>MG=NG-MN=14,2-6,2=8 (m)
Vậy S(MGE)=1/2.EG.MG=1/2.3.8=12 (m2)
=>S(ABCD)+S(ABGN)=2. S(ABCD)
=2.AB.AD=2.5.14,2=142 (m2)
=> Diện tích hình đã cho bằng:
12+142=154 m2
Đ s:
Gọi tứ giác nằm ngang là ABCD.
Hình dựng đứng là ABEMN
Từ điểm M kẻ đường thẳng//AB cắt BE tại G.
Do NM_|_AN tại A
MN//AB; BG//AN
=>BG_|_BE nên tam giác MGE vuông tại G. (1)
=>Tứ giác ABGN là hình chữ nhật=Hình chữ nhật ABCD( vì AB//=CD=14,2 m)
=>AN=AC=5 (m)
Từ (1) =>EG là đường cao của tam giác MGE có cạnh đáy MG.
=>EG=BE-BG=8-5=3 (m)
=>MG=NG-MN=14,2-6,2=8 (m)
Vậy S(MGE)=1/2.EG.MG=1/2.3.8=12 (m2)
=>S(ABCD)+S(ABGN)=2. S(ABCD)
=2.AB.AD=2.5.14,2=142 (m2)
=> Diện tích hình đã cho bằng:
12+142=154 m2


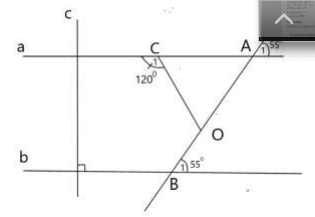
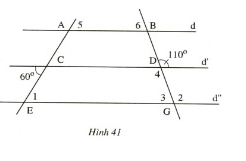
1) Tính góc ∠E1
Ta có d’//d” (gt)
⇒ ∠C = ∠E1 ( So le trong)
⇒ ∠E1 = 600 vì ∠C = 600
2) Tính ∠G3
Ta có d’//d”
⇒ ∠G2 = ∠D (Đồng vị)
⇒ ∠G1 = 1100
3) Tính ∠G3
Vì ∠G2 + ∠G3 = 1800 (kề bù)
⇒ ∠G3 = 700
4) Tính ∠D4
∠D4 = ∠D (Đối đỉnh)
⇒ ∠D4 = 1100
5) Tính ∠A5
Ta có d//d”
⇒ ∠A5 = ∠ E1 (Đồng vị)
⇒ ∠A5 = 600
6) Tính ∠B6
Ta có d//d”
⇒ ∠B6 = ∠G3 (Đồng vị)
⇒ ∠B6 = 700
 đây bạn ơi giúp mik nha
đây bạn ơi giúp mik nha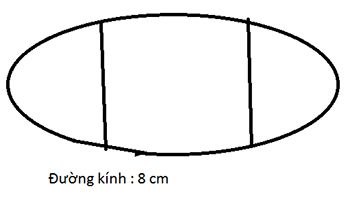




Ta có: GH//JI
=>\(\widehat{JGH}+\widehat{GJI}=180^0\)(hai góc trong cùng phía)
=>\(\widehat{JGH}=180^0-90^0=90^0\)
ta có: GH//JI
=>\(\widehat{HIJ}=\widehat{xHI}\)(hai góc so le trong)
=>\(\widehat{HIJ}=47^0\)