Trên quãng đường AC dài 200 km có một địa điểm B các A là 10 km. Lúc 7 giờ, một ô tô đi từ A, một ô tô khác đi từ B, cả hai cùng đi tới C với vận tốc thứ tự bằng 50 km/h và 40 km/h. Hỏi lúc mấy giờ thì khoảng cách đến C của xe thứ hai gấp đôi khoảng cách đến C của xe thứ nhất
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) Bài toán 1: Một ô tô đi được quãng đường 170km với vận tốc 42,5 km/giờ. Tính thời gian ô tô đi được quãng đường đó.
Bài giải:
Thời gian ô tô đi là:
170 : 42,5 = 4 (giờ)
Đáp số: 4 giờ.
Nhận xét: Để tính thời gian đi của ô tô ta lấy quãng đường đi được chia cho quãng đường ô tô đi được trong 1 giờ hay vận tốc của ô tô.
Muốn tính thời gian ta lấy quãng đường chia cho vận tốc.
Ta có: t = s : v
b) Bài toán 2: Một ca nô đi với vận tốc 36km/giờ trên quãng đường sông dài 42km. Tính thời gian đi của ca nô trên quãng đường đó.
Bài giải:
Thời gian đi của ca nô là:
42 : 36 = \(\frac{7}{6}\) (giờ)
\(\frac{7}{6}\) (giờ) = \(1\frac{1}{6}\) giờ = 1 giờ 10 phút.
Đáp số: 1 giờ 10 phút.

Gọi thời gian dự định đi hết quãng đường là x.
Độ dài quãng đường AB là: S = v.t = 40x
Nửa quãng đường là S/2 = 40x/2 = 20x.
Nửa quãng đường đầu đi vs vtốc dự định (40km/h)
=> Thời gian đi hết nửa quãng đường đầu là: t1 = S : v1 = 20x : 40 = 1/2x
Nửa quãng đường đầu đi vs vtốc tăng hơn dự định 10km/h (50km/h)
=> Thời gian đi hết nửa quãng đường sau là t2 = S : v2 = 20x : 50 = 2/5x
Tổng thời gian đi hết quãng đường là: t = t1 + t2 = 1/2x + 2/5x = 9/10x
Do thực tế đến B sớm hơn dự kiến 1h nên ta có: x - 9/10x = 1 => x = 10 (h)
=> Độ dài quãng đường AB là S = 40.10 = 400 (km).

Thời gian ô tô đi quãng đường A-B kể cả thời gian nghỉ là:
9 giờ 45 phút - 7 giờ 30 phút = 2 giờ 15 phút
Thời gian ô tô đi quãng đường A-B không kể thời gian nghỉ là:
2 giờ 15 phút - 15 phút = 2 ( giờ )
Vận tốc của ô tô là:
100 : 2 = 50 ( km/giờ )
Vận tốc xe máy là:
50 x 60% = 30 ( km/giờ )
Thời gian ô tô đi quãng đường A-B kể cả thời gian nghỉ là:
9 giờ 45 phút - 7 giờ 30 phút = 2 giờ 15 phút
Thời gian ô tô đi quãng đường A-B không kể thời gian nghỉ là:
2 giờ 15 phút - 15 phút = 2 ( giờ )
Vận tốc của ô tô là:
100 : 2 = 50 ( km/giờ )
Vận tốc xe máy là:
50 x 60% = 30 ( km/giờ )
Đáp số: 30 km/giờ
(tick dùm mik ạ)

Gọi vận tốc ô tô dự định đi quãng đường AB là x (km/h).
Có phương trình: 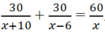
Giải ra được x = 30
Thời gian ô tô dự định đi là 2 giờ.

Gọi vận tốc xe máy là x (km/h). Điều kiện x>0
Do vận tốc xe ô tô lớn hơn vận tốc xe máy là 10km/h nên vận tốc ô tô là x+10 (km/h).
Thời gian xe máy đi từ A đến B là 120 x (h)
Thời gian ô tô đi từ A đến B là 120 x + 10 (h)
Xe ô tô đến B sớm hơn xe máy 36 phút =3/5(h) nên ta có phương trình:
120 x − 120 x + 10 = 3 5 ⇔ 120.5. x + 10 − 120.5. x = 3 x . x + 10 ⇔ 3 x 2 + 30 x − 6000 = 0 ⇔ x + 50 x − 40 = 0 ⇔ x = − 50 x = 40
Kết hợp với điều kiện đầu bài ta được x= 40.
Vậy vận tốc của xe máy là 40 (km/h), vận tốc của ô tô là 50(km/h).

Giải
Đổi 54phút = \(\frac{9}{10}\)giờ
36 phút = \(\frac{6}{10}\)giờ
Vận tốc lên dốc là :
15,3 : \(\frac{9}{10}\)= 15,3 x \(\frac{10}{9}\)= 17 ( km/ giờ )
vận tốc xuống dốc là :
24 :\(\frac{6}{10}\)= 24 x \(\frac{10}{6}\)= 40 ( km / giờ)
b) vận tốc trung bình là :
\(\frac{15,3+24}{\frac{9}{10}+\frac{6}{10}}\) = \(\frac{39,3}{\frac{15}{10}}\)= \(\frac{39,3\times10}{15}\)= 26,2 km/giờ
vậy vận tốc trung bình là 26,2 km / giờ
Ta có : 54 phút = 0,9 giờ .
36 phút = 0,6 giờ .
Vận tốc khi lên dốc là :
15,3 : 0,9 = 17 ( km / giờ )
Vận tốc khi xuống dốc là :
24 : 0,6 = 40 ( km / giờ )
Vận tốc trung bình ô tô của quãng đường là :
( 40 + 17 ) : 2 = 28,5 ( km / giờ )
Đáp số : a , 17 km / giờ .
40 km / giờ .
b , 28,5 km / giờ .

Bạn xem lời giải tại đường link dưới nhé
Câu hỏi của Anh Aries - Toán lớp 8 - Học toán với OnlineMath