Cho tam giác ABC : AB=5cm, AC=12cm, BC = 13cm. M,N lần lượt là trung điểm của AC,BC. Tính góc AMN
Nhanh nhanh nha!!!!!
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
8 tháng 11 2018
a, \(\Delta ABC\)có:
\(AB^2+AC^2=5^2+12^2=169=13^2=BC^2\)
\(\Rightarrow\Delta ABC\)vuông tại A có AM là đường trung tuyến AM ứng với cạnh huyền BC
\(\Rightarrow AM=\frac{1}{2}BC=\frac{1}{2}.13=6,5\left(cm\right)\)
b, \(\Delta ABC\)có MD là đường trung bình \(\Rightarrow MD//AB\Rightarrow MD\perp AC\left(AB\perp AC\right)\Rightarrow\widehat{ADM}=90^0\)
Tương tự \(\widehat{AEM}=90^0\)
\(\widehat{BAC}=90^0\Rightarrow\widehat{DAE}=90^0\)
Tứ giác AEMD có \(\widehat{DAE}=\widehat{ADM}=\widehat{AEM}=90^0\)
Do đó: AEMD là hình chữ nhật.
8 tháng 11 2018
a) Ta có : AB2 + AC2 = 52 + 122 = 169 = 132 = BC2
=> tam giác ABC vuông tại A ( định lý Pytago đảo )
=> AM là đường trung tuyến ứng với cạnh huyền BC
=> BM = MC = AM = 13/2 = 6,5 ( cm )
Vậy AM = 6,5 cm
b) Xét tam giác ABM có BM = AM ( chứng minh trên )
=> tam giác ABM cân tại M
Xét tam giác ABM cân tại M có DM là đường trung tuyến
=> DM đồng thời là đường cao
=> DM ⊥ AB
=> góc ADM = 900
Chứng minh tương tự ta có ME là đường cao trong tam giác cân AMN
=> góc MEA = 900
Xét tứ giác AEMD có góc ADM = góc DAE = góc MEA = 900
=> tứ giác AEMD là hình chữ nhật
H9
HT.Phong (9A5)
CTVHS
8 tháng 8 2023
a) Ta có: \(BC=13cm\Rightarrow BC^2=13^2cm=169cm\)
Xét: \(AB^2+AC^2=5^2+12^2=25+144=169=13^2=BC^2\)
Vậy tam giác ABC vuông tại A có cạnh huyền BC
b) Áp dụng định lý thích hai cạnh góc vuông tà tích giữa cạnh huyền và đường cao ta có:
\(AH\cdot BC=AB\cdot AC\)
\(\Rightarrow AH=\dfrac{AB\cdot AC}{BC}=\dfrac{12\cdot5}{13}\approx4,6\left(cm\right)\)
c) Xét ΔAHB vuông tại H có đường cao HE ta có:
\(\Rightarrow AH^2=AE\cdot AB\) (1)
Xét ΔAHC vuông tại H có đường cao HF ta có:
\(\Rightarrow AH^2=AF\cdot AC\) (2)
Từ (1) và (2)
\(\Rightarrow AB\cdot AE=AC\cdot AF\)
\(\Rightarrow\dfrac{AB}{AF}=\dfrac{AC}{AE}\) (3)
Dựa vào (3)
Ta suy ra: \(\Delta AEF\sim\Delta ABC\)
\(\Rightarrow\widehat{AEF}=\widehat{ABC}\) (đpcm)
8 tháng 8 2023
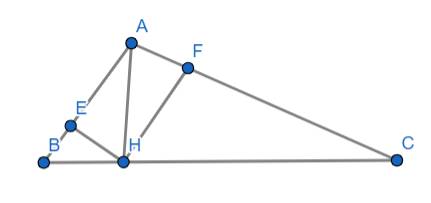
a: Xét ΔÂBC có BC^2=AB^2+AC^2
nên ΔABC vuông tại A
b: AH=AB*AC/BC=60/13(cm)
c: ΔAHB vuông tại H có HE là đường cao
nên AE*AB=AH^2
ΔAHC vuông tại H có HF là đường cao
nên AF*AC=AH^2
=>AE*AB=AF*AC
=>AE/AC=AF/AB
=>ΔAEF đồng dạng với ΔACB
=>góc AFE=góc ABC
2 tháng 3 2022
a, Ta có:\(AB^2+AC^2=12^2+16^2=400\)(cm)
\(BC^2=20^2=400\)(cm)
\(\Rightarrow AB^2+AC^2=BC^2\)
\(\Rightarrow\Delta ABC\) vuông tại A
Xét Δ DNC và Δ ABC có:
\(\widehat{NDC}=\widehat{BAC}\left(=90^o\right)\)
Chung \(\widehat{C}\)
⇒Δ DNC \(\sim\) Δ ABC (g.g)
b, Ta có: BD=DC=1/2.BC=1/2.20=10(cm)
Δ DNC \(\sim\) Δ ABC (cma)
\(\Rightarrow\dfrac{ND}{AB}=\dfrac{NC}{BC}=\dfrac{DC}{AC}\Rightarrow\dfrac{ND}{12}=\dfrac{NC}{20}=\dfrac{10}{16}\Rightarrow\left\{{}\begin{matrix}ND=7,5\left(cm\right)\\NC=12,5\left(cm\right)\end{matrix}\right.\)
c, Xét Δ DBM và Δ ABC có:
Chung \(\widehat{B}\)
\(\widehat{BDM}=\widehat{BAC}\left(=90^o\right)\)
⇒Δ DBM \(\sim\) Δ ABC(g.g)
\(\Rightarrow\dfrac{MB}{BC}=\dfrac{BD}{AB}\Rightarrow\dfrac{MB}{20}=\dfrac{10}{12}\Rightarrow MB=\dfrac{50}{3}\left(cm\right)\)
Ta có: MD⊥BC, BD=DC ⇒ ΔBDC cân tại M
\(\Rightarrow MB=MC=\dfrac{50}{3}\left(cm\right)\)
10 tháng 4 2021
a) Xét ΔAHB vuông tại H và ΔAHC vuông tại H có
AB=AC(ΔBAC cân tại A)
AH chung
Do đó: ΔAHB=ΔAHC(cạnh huyền-cạnh góc vuông)
Suy ra: BH=HC(hai cạnh tương ứng)
NA
29 tháng 11 2016
Áp dụng định lí pitago vào tgiac ABH vuông tại H có:
BH^2=AB^2-AH^2=!3^2-12^2=25
=>BH=5(cm)
Áp dụng định lí pitago vào tam giác AHC vuông tại H có:
AC^2=AH^2+HC^2=12^2+16^2=400
=> AC=20(cm)
Ta có HM=AM=MC( vì trong một tam giác vuông đường trung tuyến ứng với cạnh huyền thì bằng nửa cạnh huyền)
=> HM=10(cm)
*** cho mk nha ^^!
14 tháng 7 2023
Xét ΔABC có AD là phân giác
nên BD/AB=CD/AC
=>BD/2=CD/3=(BD+CD)/(2+3)=15/5=3
=>BD=6cm và CD=9cm
Xét ΔBAD có BI là phân giác
nên AI/ID=AB/BD=2
=>AI/AD=2/3=AG/AM
=>IG//BC
14 tháng 7 2023
Xét ΔABC có AD là phân giác
nên BD/AB=CD/AC
=>BD/2=CD/3=(BD+CD)/(2+3)=15/5=3
=>BD=6cm và CD=9cm
Xét ΔBAD có BI là phân giác
nên AI/ID=AB/BD=2
=>AI/AD=2/3=AG/AM
=>IG//BC
rorry mình lười giải