MN giúp mik bài này với ạ.Mik cảm ơn trước:
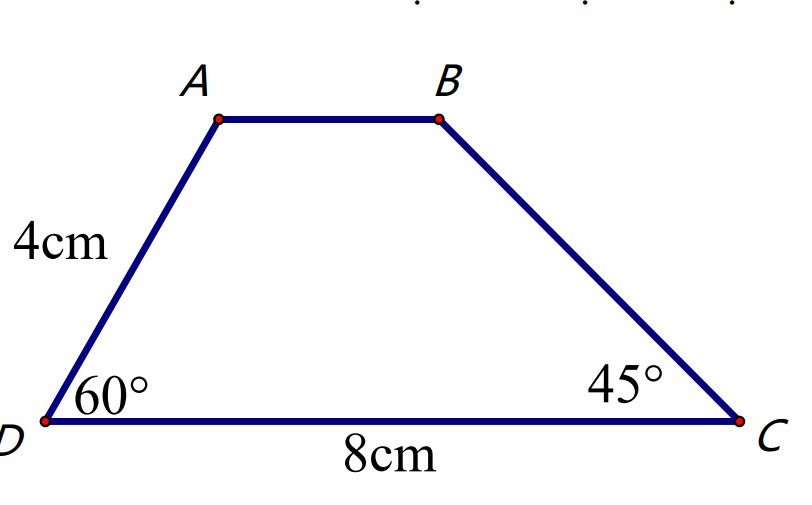
Cho hình vẽ. Tính các cạnh còn lại của hình thang
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Có hình thang cân ABCD (gt)
có A+D=180 ĐỘ
A+60=180
=) A=180-60
A=120
Có hình thang cân ABCD
AB//CD (gt)
Từ hai điều trên =) ^D=^C
Mà D=60
Từ hai điều này =)c=60
=) A=B
Mà A = 120(cmt)
Từ hai điều này =) B = 120
Hình thang ABCD là hình thang cân
Mà AB//CD(gt)
=)BC=AD (tính chất htang cân * câu này k cần viết cũng được)
Mà Bc=5cm
Từ hai điều này =)AD= 5cm
Có hình thang cân ABCD
AD=BC
Từ hai điều này =) AB=DC
Mà AB = 3 cm
=) Dc =3cm

ABCD là hình thang cân
=>góc ADC=góc DCB=180-60=120 độ
AB//CD
=>góc KCB=góc CBA=60 độ
Xét tứ giác ABKH có
KH//AB
AH//BK
Do đó: ABKH là hình bình hành
=>AB=KH=8cm
Xét ΔAHD vuông tại H và ΔBKC vuông tại K có
AD=BC
góc ADH=góc BCK
Do đó: ΔAHD=ΔBKC
=>HD=KC=2cm
HD+DC+CK=HK
=>2+2+DC=8
=>DC=4(cm)

BÀI 2; Cho hình cân ABCD ( AB // CD ) ; góc A = 120 độ. Tính các góc còn lại của hình thang.
Giải:
Xét hình thang cân ABCD ta có:
góc BAD + góc ADC = 180 độ ( 2 góc trong cùng phía bù nhau do AB//CD)
=> 120 độ + góc ADC = 180 độ
=> góc ADC = 60 dộ
Vì tiws giác ABCD là hình thang cân
=> góc BAD = góc ABC = 120 độ
=> góc ADC = góc BCD = 60 độ

bạn tự vẽ hình nhé !
xét AD // BC . vì góc BDC = 30 độ => góc ABD = 30 độ (hai goc so le trong)
mà AD = AB => tam giác ABD cân tại A => góc ADB = 30 độ . vậy góc D = 60 độ
A + D = 180 độ (hai góc trong cùng phía ) => A = 180 - 60 = 120 độ
=> góc B = 60 độ , C = 120 độ

230 đó bn
trong violympic vòng 16 chứ gì
tk mk nhé mk nhanh nhất
A B C D H K
Dựng \(AH\perp CD;BK\perp CD\left(H;K\in CD\right)\)
Xét tg vuông ADH có
\(\widehat{DAH}=90^o-\widehat{D}=30^o\)
\(\Rightarrow DH=\dfrac{AD}{2}=\dfrac{4}{2}=2cm\) (trong tg vuông cạnh đối diện góc \(30^o\) băng nửa cạnh huyền)
\(\Rightarrow AH=\sqrt{AD^2-DH^2}=\sqrt{16-4}=\sqrt{12}=2\sqrt{3}cm\)
\(\Rightarrow AH=BK=2\sqrt{3}cm\) (đường cao của hình thang)
Xét tg vuông BCK có
\(\widehat{KBC}=90^o-\widehat{C}=45^o\)
=> tg BCK vuông cân tại K \(\Rightarrow CK=BK=2\sqrt{3}cm\)
\(\Rightarrow BC=\sqrt{BK^2+CK^2}=\sqrt{12+12}=2\sqrt{6}cm\)
Xét HCN ABKH có
\(AB=KH=CD-DH-CK=8-2\sqrt{3}-2\sqrt{3}=8-4\sqrt{3}=4\left(2-\sqrt{3}\right)cm\)