Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Do góc <DAB = <CBD =90 độ và <ABD = < BDC (do AB//CD)
-> Tam giác ADB và BCD đồng dạng
=> AD/BC = DB/CD <-> AD.CD=BC.DB <-> BC.DB = 12.25 =300 (1)
Mặt khác do tam giác DBC vuông tại B nên theo định lý Pitago :
BD^2+BC^2=CD^2
hay BC^2+BD^2 =625 (2)
Từ (1) và (2) ta giải hệ thì có BC, BD:
BD^2+ (300/BD)^2=625 -> BD^4 - 625 BD^2 +900 = 0 -> BD^2 = (625+can( 387025))/2 ( loại nghiệm còn lại do BD là cạnh huyền của tam giác vuông ABD nên BD^2 > AD^2 =144)
-> BD = can( (625+can( 387025))/2 )
-> BC = 3000/BD
Do góc <DAB = <CBD =90 độ và <ABD = < BDC (do AB//CD)
-> Tam giác ADB và BCD đồng dạng
=> AD/BC = DB/CD <-> AD.CD=BC.DB <-> BC.DB = 12.25 =300 (1)
Mặt khác do tam giác DBC vuông tại B nên theo định lý Pitago :
BD^2+BC^2=CD^2
hay BC^2+BD^2 =625 (2)
Từ (1) và (2) ta giải hệ thì có BC, BD:
BD^2+ (300/BD)^2=625 -> BD^4 - 625 BD^2 +900 = 0 -> BD^2 = (625+can( 387025))/2 ( loại nghiệm còn lại do BD là cạnh huyền của tam giác vuông ABD nên BD^2 > AD^2 =144)
-> BD = can( (625+can( 387025))/2 )
-> BC = 3000/BD
~~~~~~~~~~~ai đi ngang qua nhớ để lại k ~~~~~~~~~~~~~
~~~~~~~~~~~~ Chúc bạn sớm kiếm được nhiều điểm hỏi đáp ~~~~~~~~~~~~~~~~~~~
~~~~~~~~~~~ Và chúc các bạn trả lời câu hỏi này kiếm được nhiều k hơn ~~~~~~~~~~~~

Áp dụng các hệ thức lượng trong tam giác vuông BDC cùng chú ý độ dài đường cao hạ từ B xuống CD bằng AD, ta tính được : AB = 9cm, BD =15cm, hoặc AB = 16cm, BC = 15cm, BD = 20cm

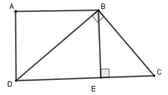
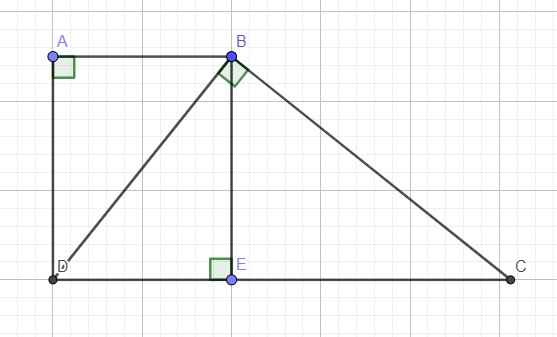
Kẻ BE ⊥ CD tại E
Suy ra tứ giác ABED là hình chữ nhật (vì A ^ = D ^ = E ^ = 90 ∘ ) nên BE = AD = 12cm
Đặt EC = x (0 < x < 25) thì DE = 25 – x
Áp dụng hệ thức giữa cạnh và đường cao trong tam giác vuông BCD ta có:
B E 2 = E D . E C ⇔ x ( 25 - x ) = 144 ⇔ x 2 - 25 x + 144 = 0
x 2 - 16 x - 9 x + 144 = 0 <=> x(x – 16) – 9(x – 16) = 0 <=> (x – 16)(x – 9) = 0
⇔ x = 16 x = 9 (thỏa mãn)
Với EC = 16, theo định lý Pytago ta có BC = B E 2 + E C 2 = 12 2 + 16 2 = 20 (loại)
Với EC = 9, theo định lý Pytago ta có BC = B E 2 + E C 2 = 12 2 + 9 2 = 15 (nhận)
Vậy BC = 15cm
Đáp án cần chọn là: A

Kẻ BE vuông góc CD \(\Rightarrow ABED\) là hcn (tứ giác 4 góc vuông) \(\Rightarrow AB=DE\)
Đặt \(AB=x>0\)
Áp dụng định lý Pitago cho tam giác vuông ABD:
\(AB^2+AD^2=BD^2\Leftrightarrow BD^2=x^2+144\) (1)
Áp dụng hệ thức lượng cho tam giác vuông BDC:
\(BD^2=DE.DC\Leftrightarrow BD^2=25x\) (2)
(1);(2) \(\Rightarrow x^2+144=25x\Rightarrow x^2-25x+144=0\Rightarrow\left[{}\begin{matrix}x=16\\x=9\end{matrix}\right.\)
- Với \(AB=16\left(cm\right)\Rightarrow BD=\sqrt{AD^2+AB^2}=20\left(cm\right)\)
\(BC=\sqrt{DC^2-BD^2}=15\left(cm\right)\)
- Với \(AB=9\left(cm\right)\Rightarrow BD=\sqrt{AD^2+AB^2}=15\left(cm\right)\)
\(BC=\sqrt{DC^2-BD^2}=20\left(cm\right)\)

Kẻ đường cao BH
Xét tứ giác ABHD có
\(\widehat{BAD}=90^0\)
\(\widehat{ADH}=90^0\)
\(\widehat{BHD}=90^0\)
Do đó: ABHD là hình chữ nhật(Dấu hiệu nhận biết hình chữ nhật)
Áp dụng định lí Pytago vào ΔABD vuông tại A, ta được:
\(BD^2=AB^2+AD^2\)
\(\Leftrightarrow AB^2+12^2=BD^2\)(1)
Ta có: ABHD là hình chữ nhật(cmt)
nên AD=BH(hai cạnh đối)
mà AD=12cm(gt)
nên BH=12cm
Áp dụng định lí Pytago vào ΔBDC vuông tại B, ta được:
\(DC^2=BD^2+BC^2\)
\(\Leftrightarrow BD^2+BC^2=25^2=625\)(2)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔBDC vuông tại B có BH là đường cao ứng với cạnh huyền DC, ta được:
\(BD\cdot BC=BH\cdot DC\)
\(\Leftrightarrow BD\cdot BC=12\cdot25=300\)
hay \(BC=\dfrac{300}{BD}\)(3)
Thay (3) vào (2), ta được:
\(BD^2+\left(\dfrac{300}{BD}\right)^2=625\)
\(\Leftrightarrow\dfrac{BD^4+90000}{BD^2}=625\)
\(\Leftrightarrow BD^4-625BD^2+90000=0\)
\(\Leftrightarrow BD^4-400BD^2-225BD^2+90000=0\)
\(\Leftrightarrow\left(BD^2-400\right)\left(BD^2-225\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}BD=15\\BD=20\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}AB=9\left(cm\right)\\AB=16\left(cm\right)\end{matrix}\right.\)
Diện tích hình thang ABCD là:
\(S_{ABCD}=\dfrac{AB+CD}{2}\cdot AD=\left[{}\begin{matrix}\dfrac{9+25}{2}\cdot12=204\left(cm^2\right)\\\dfrac{9+16}{2}\cdot12=150\left(cm^2\right)\end{matrix}\right.\)
từ B hạ BE\(\perp DC\)
theo bài ra ABCD là hình thang \(=>AB//CD=>AB//DE\)
mà \(\angle\left(A\right)=\angle\left(D\right)=90^o\)=>chứng minh được ABED là hình chữ nhật
\(=>AD=BE=12cm\)
áp dụng hệ thức lượng \(=>BE^2=DE.EC< =>12^2=DE\left(25-DE\right)=>DE=16cm=AB\)
\(=>S\left(ABCD\right)=\dfrac{\left(AB+CD\right)BE}{2}=\dfrac{\left(16+25\right)12}{2}=246cm^2\)