Cho biết đường trung trực là gì?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
N
3
5 tháng 5 2019
Đường cao của tam giác là đoạn vuông góc kẻ từ một đỉnh đến cạnh đối diện. Cạnh đối diện này được gọi là đáy ứng với đường cao. Độ dài của đường cao là khoảng cách giữa đỉnh và đáy.
Trong hình học phẳng, đường trung trực của một đoạn thẳng là đường vuông góc với đoạn thẳng tại trung điểm của đoạn thẳng đó.Trong đường tròn, giao 2 tiếp tuyến thì điểm đó đến tâm là đường trung trực.
đường trung tuyến là một đường thẳng nối từ đỉnh của một tam giác tới trung điểm của cạnh tam giác đối diện.
5 tháng 5 2019
Đường cao của tam giác là đoạn vuông góc kẻ từ một đỉnh đến cạnh đối diện
đường trung trực của một đoạn thẳng là đường vuông góc với đoạn thẳng tại trung điểm của đoạn thẳng đó
trung tuyến của một tam giác là một đoạn thẳng nối từ đỉnh của tam giác tới trung điểm của cạnh đối diện
KH
12 tháng 5 2017
1.
Đường trung trực của đoạn thẳng là đường vuông góc với đường thẳng đó tại trung điểm.
2.
Những điểm thuộc đường trung trực của 1 đoạn thẳng thì luôn cách đều 2 mút của đoạn thẳng đó.
3.
Những điểm cách đều 2 mút của 1 đoạn thẳng thì nằm trên đường trung trực của đoạn thẳng ấy.
KH
12 tháng 5 2017
1.
Đường trung trực của đoạn thẳng là đường vuông góc với đường thẳng đó tại trung điểm.
2.
Những điểm thuộc đường trung trực của 1 đoạn thẳng thì luôn cách đều 2 mút của đoạn thẳng đó.
3.
Những điểm cách đều 2 mút của 1 đoạn thẳng thì nằm trên đường trung trực của đoạn thẳng ấy.
PT
Cho đường tròn (O), bán kính OA, dây CD là đường trung trực của OA. Tứ giác OCAD là hình gì? Vì sao?
1
CM
15 tháng 2 2017
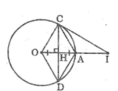
Gọi H là giao điểm của OA và CD
Vì CD là đường trung trực của OA nên:
CD ⊥ OA và HA = HO
Mà CD ⊥ OA nên HC = HD (đường kính dây cung)
Vì tứ giác ACOD có hai đường chéo cắt nhau tại trung điểm mỗi đường nên nó là hình bình hành.
Dồng thời CD ⊥ OA nên ACOD là hình thoi
22 tháng 9 2021
c: Đường trung trực của hai đoạn nói trên giao nhau tại O
15 tháng 10 2017
Đường trung trực của đoạn thẳng là 1 đường thẳng vuông góc với đoạn thẳng và đi qua trung điểm của đoạn thẳng đó. Tính chất của đường trung trực của đoạn thẳng: Điểm nằm cách đều hai mút của đoạn thẳng thì nằm trên đường trung trực của đoạn thẳng
CM
28 tháng 10 2017
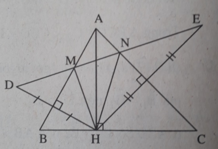
M thuộc đường trung trực của HD nên MH = MD. MB là đường trung trực của đáy HD của tam giác cân HMD nên MB là tia phân giác của góc HMD. Tương tự NC là tia phân giác của góc HNE. Vậy MB, NC là các đường phân giác góc ngoài của ΔHMN.
Các đường thẳng MB, NC cắt nhau tại A nên HA là đường phân giác trong của góc MHN của ΔHMN.
+) HC vuông góc với HA tại H mà HA là đường phân giác trong của góc MHN nên HC là đường phân giác góc ngoài của ΔHMN.( đường phân giác góc trong và góc ngoài tại 1 đỉnh của 1 tam giác vuông góc với nhau)
+) Các đường thẳng HC và NC cắt nhau tại C; HC và NC là hai đường phân giác ngoài của tam giác HMN nên MC là đường phân giác góc trong của ΔHMN.
MB và MC là các tia phân giác của hai góc kề bù ∠DMH; ∠HMA nên MB ⊥ MC.
Vậy MC ⊥ AB.
Định lý
Trong mặt phẳng, tập hợp tất cả các điểm mà khoảng cách từ điểm đó tới hai đầu mút của đoạn thẳng bằng nhau được gọi là đường trung trực của đoạn thẳng đó.
Tính chất
Điểm nằm cách đều hai mút của đoạn thẳng thì nằm trên đường trung trực của đoạn thẳng đó. Ngược lại, điểm nằm trên đường trung trực của một đoạn thẳng thì cách đều hai mút của đoạn thẳng đó.
Trong đoạn thẳng
Điểm nằm trên đường trung trực của một đoạn thẳng thì cách đều hai mút của đoạn thẳng đó
Trong tam giác
Đường trung trực của cạnh của tam giác là đường trung trực của tam giác.
Trong tam giác, ba đường trung trực đồng quy tại một điểm, điểm đó cách đều 3 đỉnh của Tam giác và là tâm đường tròn ngoại tiếp tam giác.
Trong tam giác vuông tâm đường tròn ngoại tiếp là trung điểm của cạnh huyền.
Trong tam giác cân, đường trung trực của cạnh đáy đồng thời là đường trung tuyến tương ứng với cạnh này.
Trong không gian 3 chiều, quỹ tích này mở rộng thành mặt phẳng trung trực của đoạn thẳng.
Từ trung điểm của một cạnh bất kì, kẻ đường thẳng vuông góc với cạnh đang xét
Bằng compa, quay 2 vòng tròn có tâm là 2 đầu đoạn thẳng, bán kính bằng độ dài đoạn thẳng (hoặc ít nhất là lớn hơn nửa độ dài đoạn thẳng). Đường trung trực là đường nối giao điểm hai vòng tròn này.
Khái niệm đường trung trực của đoạn thẳng:
-Đường trung trực của đoạn thẳng là 1 đường thẳng vuông góc với đoạn thẳng và đi qua trung điểm của đoạn thẳng đó.
Tính chất của đường trung trực của đoạn thẳng:
-Điểm nằm cách đều hai mút của đoạn thẳng thì nằm trên đường trung trực của đoạn thẳng đó. Ngược lại, điểm nằm trên đường trung trực của một đoạn thẳng thì cách đều hai mút của đoạn thẳng đó.