cho x+y+z=0 và xyz khác 0 . tính P= 1/y2 + z2 - x2 + 1/x2 + y2 - z2 + 1/x2 + z2 - y2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


x2+y2−z22xy−y2+z2−x22yz+z2+x2−y22xz=1x2+y2−z22xy−y2+z2−x22yz+z2+x2−y22xz=1
Tính P = x + y + z


Ta có : \(x^2+y^2\ge2xy\)
\(\Leftrightarrow2\left(x^2+y^2\right)\ge\left(x+y\right)^2\)
\(\Leftrightarrow x^2+y^2\ge\frac{\left(x+y\right)^2}{2}\)
Áp dụng vào bài toán có :
\(P\le\frac{x+y}{\frac{\left(x+y\right)^2}{2}}+\frac{y+z}{\frac{\left(y+z\right)^2}{2}}+\frac{z+x}{\frac{\left(z+x\right)^2}{2}}\) \(=\frac{2}{x+y}+\frac{2}{y+z}+\frac{2}{z+x}=\frac{1}{2}\left(\frac{4}{x+y}+\frac{4}{y+z}+\frac{4}{z+x}\right)\)
Áp dụng BĐT Svacxo ta có :
\(\frac{4}{x+y}\le\frac{1}{x}+\frac{1}{y}\), \(\frac{4}{y+z}\le\frac{1}{y}+\frac{1}{z}\), \(\frac{4}{z+x}\le\frac{1}{z}+\frac{1}{x}\)
Do đó : \(P\le\frac{1}{2}\left[2.\left(\frac{1}{x}+\frac{1}{y}+\frac{1}{z}\right)\right]=2016\)
Dấu "=" xảy ra \(\Leftrightarrow x=y=z=\frac{1}{672}\)
P/s : Dấu "=" không chắc lắm :))

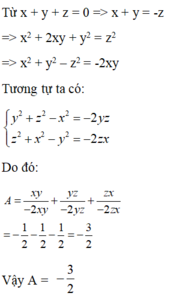
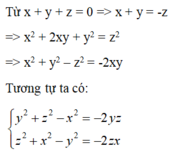
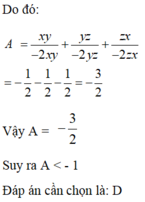
Có : \(x+y+z=0\)
\(\Leftrightarrow\left(x+y\right)=-z\)
\(\Rightarrow\left(x+y\right)^2=\left(-z\right)^2\)
\(\Rightarrow x^2+2xy+y^2=z^2\)
\(\Rightarrow x^2+y^2-z^2=-2xy\)
Tương tự : \(y^2+z^2-x^2=-2yz\)
\(z^2+x^2-y^2=-2xz\)
Suy ra :
\(P=\frac{1}{-2xy}+\frac{1}{-2yz}+\frac{1}{-2zx}=\frac{-1}{xyz}\left(x+y+z\right)=\frac{-1}{xyz}.0=0\)
Câu hỏi của Hoàng Liên - Toán lớp 9 - Học toán với OnlineMath