Cho tam giác ABC. Gọi O, G, H lần lượt là tâm đường tròn ngoại tiếp, trọng tâm. trực tâm của tam giác ABC. Gọi I là tâm đường tròn đi qua trung điểm của ba cạnh AB, BC, CA. Chứng minh:
b) HA + HB + HC = 2HO = 3HG
c) OH =2OI
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
7 tháng 4 2019
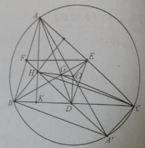
Phép vị tự tâm G tỉ số -1/2 biến A thành D; biến B thành E; biến C thành F ⇒ biến tam giác ABC thành tam giác DEF.
Đáp án B
CM
15 tháng 11 2017
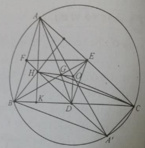
G D → = - 1 / 2 G A → ⇒ phép vị tự tâm G tỉ số -1/2 biến A thành D.
Đáp án B.
CM
12 tháng 7 2017
Gọi A’ là điểm đối xứng với A qua tâm O.
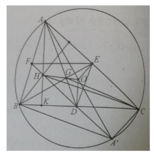
chứng minh BHCA’ là hình bình hành, suy ra H, A', D thẳng hàng và DO là đường trung bình của tam giác AHA’ ⇒ D O → = - 1 / 2 A H → ⇒ phép vị tự tâm G tỉ số -1/2 biến A H → thành DO → .
Đáp án B
CM
18 tháng 2 2018
* Do O là tâm đường tròn ngoại tiếp tam giác ABC nên O là giao điểm của 3đường trung trực của tam giác ABC.
Lại có: M là trung điểm của BC nên O M ⊥ B C (OM là 1 đường trung trực của tam giác) (1)
* Lại có H là trực tâm của tam giác ABC nên: A H ⊥ B C (2)
Từ (1) và (2) suy ra: OM // AH.
* Nếu tam giác ABC nhọn thì O nằm trong tam giác ABC nên A H → , O M → cùng hướng
* Nếu tam giác ABC tù thì O nằm ngoài tam giác ABC nên A H → , O M → ngược hướng.
Đáp án A