Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a, HCDB là hbh (gt)
-> CH // BD; HB // CD
Vì H là trực tâm của Δ ABC (gt)
-> CH vuông với AB ; BH vuông với AC ; AH vuông với BC
-> AB vuông BD ; AC vuông CD
-> ^ABD=90*, ^ ACD=90*
Xét tứ giác ABCD có: ^ABD + ^ ACD = 180*
-> tứ giác ABCD nội tiếp
-> A, B, C, D cùng thuộc 1 đường tròn (1)
DE // BC (gt)
->AH vuông DE ( vì AH vuông BC )
-> ^AED = 90*
Xét tứ giác ABED có ^AED=^ABD=90*
-> B và E cùng nhìn AD dưới 1 góc 90*
-> ABED nội tiếp
-> A,B,E,D cùng thuộc 1 đường tròn (2)
Từ (1) và (2) -> A,B,C,D,E cùng thuộc một đường tròn
b) ABEDC nội tiếp
-> ^BAE = ^BDE (2 góc nội tiếp cùng chắn cung BE)
Và ^DAC = ^DBC (2 góc nội tiếp cùng chắn cung CD)
Mà ^DBC = ^BDE (2 góc sole trong)
-> ^BAE = ^CAD

a, HCDB là hbh (gt)
-> CH // BD; HB // CD
Vì H là trực tâm của Δ ABC (gt)
-> CH vuông với AB ; BH vuông với AC ; AH vuông với BC
-> AB vuông BD ; AC vuông CD
-> ^ABD=90*, ^ ACD=90*
Xét tứ giác ABCD có: ^ABD + ^ ACD = 180*
-> tứ giác ABCD nội tiếp
-> A, B, C, D cùng thuộc 1 đường tròn (1)
DE // BC (gt)
->AH vuông DE ( vì AH vuông BC )
-> ^AED = 90*
Xét tứ giác ABED có ^AED=^ABD=90*
-> B và E cùng nhìn AD dưới 1 góc 90*
-> ABED nội tiếp
-> A,B,E,D cùng thuộc 1 đường tròn (2)
Từ (1) và (2) -> A,B,C,D,E cùng thuộc một đường tròn

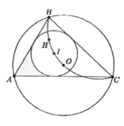
Chứng minh được B I C ^ = 120 0
=> B O C ^ = 2 B A C ^ = 120 0 => B H C ^ = 180 0 - 60 0 = 120 0 (góc nội tiếp và góc ở tâm)
=> H, I, O cùng nhìn BC dưới góc 120 0 nên B, C, O, I, H cùng thuộc một đường tròn

a: Xét (O) có
ΔABD nội tiếp
AD là đường kính
Do đó: ΔABD vuông tại B
=>BD vuông góc AB
=>BD//CH
Xét (O) có
ΔACD nội tiếp
AD là đường kính
Do đó: ΔACD vuông tại C
=>AC vuông góc CD
=>CD//BH
Xét tứ giác BHCD có
BH//CD
BD//CH
Do đó: BHCD là hình bình hành
b: BHCD là hình bình hành
=>BC cắt HD tại trung điểm của mỗi đường
=>I là trung điểm của HD
Xét ΔHDA có
I,O lần lượt là trung điểm của DH,DA
=>IO là đường trung bình
=>IO//AH và IO=AH/2
=>AH=2IO