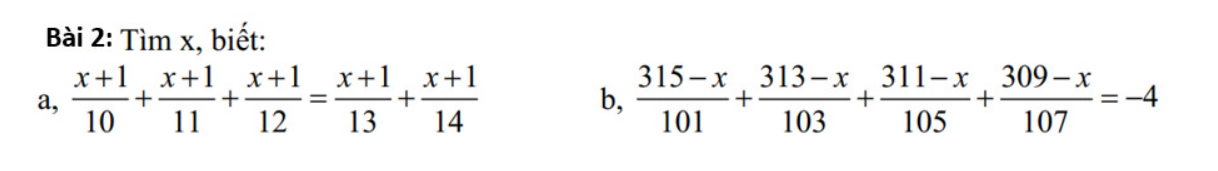 giải giúp tôi với ai giải được mình tick cho ai giải đc mình cảm ơn
giải giúp tôi với ai giải được mình tick cho ai giải đc mình cảm ơn
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đánh giá được mức đơn giản của thuật toán, từ đó tìm ra được cách giải nhanh nhất.

Số lần so sánh giữa các phần tử: Trong thuật toán sắp xếp chọn, số lần so sánh giữa các phần tử là cố định, không phụ thuộc vào dữ liệu đầu vào. Cụ thể, số lần so sánh trong thuật toán sắp xếp chọn là \(\dfrac{n\left(n-1\right)}{2}\), với n là số phần tử trong mảng hoặc danh sách.
Số lần hoán đổi giữa các phần tử: Trong thuật toán sắp xếp chọn, số lần hoán đổi giữa các phần tử có thể đạt đến tối đa n-1 lần, với n là số phần tử trong mảng hoặc danh sách.
Vậy độ phức tạp thời gian của thuật toán sắp xếp chọn là O(n2), hay \(\dfrac{n\left(n-1\right)}{2}\) lần so sánh và tối đa n-1 lần hoán đổi giữa các phần tử.


Thuật toán là một chuỗi các bước được thiết kế để giải quyết một vấn đề cụ thể. Một trong những yếu tố quan trọng để đánh giá hiệu suất của một thuật toán là độ phức tạp thời gian, tức là thời gian mà thuật toán mất để thực thi dựa trên kích thước đầu vào của vấn đề. Phân loại thuật toán dựa trên độ phức tạp thời gian là một phương pháp được sử dụng phổ biến để đánh giá và so sánh hiệu suất của các thuật toán khác nhau. Dưới đây là một số phân loại chính dựa trên độ phức tạp thời gian của thuật toán:
-O(1) (độ phức tạp thời gian hằng số): Đây là loại thuật toán có thời gian thực thi không thay đổi theo kích thước đầu vào. Thời gian thực thi của thuật toán này là cố định, vì vậy độ phức tạp thời gian là hằng số. Ví dụ: Truy cập vào phần tử trong mảng có kích thước cố định.
-O(log n) (độ phức tạp thời gian logarithmic): Đây là loại thuật toán có thời gian thực thi tăng theo logarit của kích thước đầu vào. Thuật toán này thường được sử dụng trong các bài toán tìm kiếm nhị phân, các thuật toán chia để trị, hoặc các thuật toán sắp xếp hiệu quả như QuickSort hoặc MergeSort.
-O(n) (độ phức tạp thời gian tuyến tính): Đây là loại thuật toán có thời gian thực thi tăng tỷ lệ trực tiếp với kích thước đầu vào. Ví dụ: Duyệt qua từng phần tử trong mảng một lần.
-O(n2) (độ phức tạp thời gian bậc hai): Đây là loại thuật toán có thời gian thực thi tăng theo bình phương của kích thước đầu vào. Ví dụ: Thuật toán sắp xếp Bubble Sort, các thuật toán tìm kiếm không hiệu quả như Linear Search trong một mảng lồng nhau.
-O(nk) (độ phức tạp thời gian bậc k): Đây là loại thuật toán có thời gian thực thi tăng theo lũy thừa của kích thước đầu

Chương trình trên tính số lần lặp cần thiết để i lớn hơn n bằng cách nhân i với 2 trong mỗi lần lặp, sau đó tăng biến sum lên 1. Để xác định độ phức tạp thời gian của chương trình này, ta cần xem xét số lần lặp của vòng while và các phép toán trong vòng lặp.
Vòng while: Vòng lặp này chạy cho đến khi i >= n, và giá trị ban đầu của i là 1. Trong mỗi lần lặp, i được nhân với 2, vậy số lần lặp là log2(n) (vì sau mỗi lần nhân i với 2, giá trị của i sẽ gấp đôi). Ví dụ, nếu n = 1000 thì số lần lặp là log2(1000) ≈ 10.
Các phép toán trong vòng lặp:
Phép gán i = i * 2: Đây là phép nhân, có độ phức tạp là O(1).
Phép gán sum = sum + 1: Đây là phép gán giá trị vào biến sum, có độ phức tạp là O(1).
Vậy tổng độ phức tạp thời gian của chương trình là O(log n), hay O(log2(1000)) ≈ O(10)

\(715-1288:x-469+1127:x=295\)
\(=>\left(715-469\right)-\left(1288-1127\right):x=295\)
\(=>246-161:x=295\)
\(=>161:x=-49\) (vô lí)
Đề bài sai.
\(161:x=-49\)
\(\Rightarrow x=-\dfrac{161}{49}\)
Để không sai nhé vẫn tính được


Sau lần chia đôi đầu tiên, pham vi tìm kiếm còn lại n/2 số, sau khi chia đôi lần thứ hai, dãy còn lại n/4 số, sau khi chia đôi lần thứ dãy còn lại n/8, …sau khi chia đôi lần k dãy còn lại n/2.mũ k. Kết thúc khi 2 mũ k sấp xỉ n.

Đề : Một hình chữ nhật có chu vi bằng 80 cm. Tăng chiều rộng lên 3cm; tăng chiều dài lên 5 cm thì diện tích tăng thêm 195 cm^2.
Tìm chiều dài và chiều rộng ban đầu.

#include <bits/stdc++.h>
using namespace std;
int a,b,x;
int main()
{
cout<<"Nhap a: ";
cin>>a;
cout<<"Nhap b: ";
cin>>b;
if(a==0)
{
if(b==0)
{
cout<<"Phuong trinh vo so nghiem"<<endl;
}
else
{
cout<<"Phuong trinh vo nghiem"<<endl;
}
}
else
{
x=-b/a;
cout<<"Phuong trinh co nghiem la: "<<x<<endl;
}
Return 0;
}


a)
\(\dfrac{x+1}{10}+\dfrac{x+1}{11}+\dfrac{x+1}{12}=\dfrac{x+1}{13}+\dfrac{x+1}{14}\\ \Rightarrow\dfrac{x+1}{10}+\dfrac{x+1}{11}+\dfrac{x+1}{12}-\dfrac{x+1}{13}-\dfrac{x+1}{14}=0\\ \Rightarrow\left(x+1\right)\cdot\left(\dfrac{1}{10}+\dfrac{1}{11}+\dfrac{1}{12}-\dfrac{1}{13}-\dfrac{1}{14}\right)=0\)
Vì \(\dfrac{1}{10}+\dfrac{1}{11}+\dfrac{1}{12}-\dfrac{1}{13}-\dfrac{1}{14}\ne0\) nên:
\(x+1=0\\ \Rightarrow x=-1\)
Vậy...
b) \(\dfrac{315-x}{101}+\dfrac{313-x}{103}+\dfrac{311-x}{105}+\dfrac{309-x}{107}=-4\\ \Rightarrow\dfrac{315-x}{101}+\dfrac{313-x}{103}+\dfrac{311-x}{105}+\dfrac{309-x}{107}+4=0\\ \Rightarrow\left(\dfrac{315-x}{101}+1\right)+\left(\dfrac{313-x}{103}+1\right)+\left(\dfrac{311-x}{105}+1\right)+\left(\dfrac{309-x}{107}+1\right)=0\\ \Rightarrow\dfrac{416-x}{101}+\dfrac{416-x}{103}+\dfrac{416-x}{105}+\dfrac{416-x}{107}=0\\ \Rightarrow\left(416-x\right)\left(\dfrac{1}{101}+\dfrac{1}{103}+\dfrac{1}{105}+\dfrac{1}{107}\right)=0\)
Vì \(\dfrac{1}{101}+\dfrac{1}{103}+\dfrac{1}{105}+\dfrac{1}{107}\ne0\) nên:
\(416-x=0\\ \Rightarrow x=416\)
Vậy...