
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: \(x\left(x-y\right)+y\left(x+y\right)\)
\(=x^2-xy+xy+y^2\)
\(=x^2+y^2\)
=100
b: \(x\left(x^2-y\right)-x^2\left(x+y\right)+y\left(x^2-x\right)\)
\(=x^3-xy-x^3-x^2y+x^2y-xy\)
\(=-2xy\)

a) phân thức xác định khi \(x^3+8\ne0\Leftrightarrow x^3\ne-8\Leftrightarrow x\ne-2\)
b)\(\frac{2x^2-4x+8}{x^3+8}=\frac{2\left(x^2-2x+4\right)}{\left(x+2\right)\left(x^2-2x+4\right)}=\frac{2}{x+2}\)
c) \(\frac{2}{x+2}=\frac{2}{2+2}=\frac{2}{4}=\frac{1}{2}\)
d)\(\frac{2}{x+2}=2\Leftrightarrow x+2=1\Leftrightarrow x=-1\)

ĐK \(x\ne\left\{-2;2\right\}\)
a. Ta có \(A=\left(\frac{x}{\left(x+2\right)\left(x-2\right)}-\frac{2}{x-2}+\frac{1}{x+2}\right):\left(x-2+\frac{10-x^2}{x+2}\right)\)
\(=\frac{x-2x-4+x-2}{\left(x+2\right)\left(x-2\right)}:\frac{x^2-4+10-x^2}{x+2}=-\frac{6}{\left(x-2\right)\left(x+2\right)}.\frac{x+2}{6}=-\frac{1}{x-2}\)
b. Ta có \(\left|x\right|=\frac{1}{2}\Rightarrow\orbr{\begin{cases}x=\frac{1}{2}\\x=-\frac{1}{2}\end{cases}}\)
Với \(x=\frac{1}{2}\Rightarrow A=\frac{-1}{\frac{1}{2}-2}=\frac{2}{3}\)
Với \(x=-\frac{1}{2}\Rightarrow A=\frac{-1}{-\frac{1}{2}-2}=\frac{2}{5}\)
c. Để \(A< 0\Rightarrow-\frac{1}{x-2}< 0\Rightarrow x-2>0\Rightarrow x>2\)
Vậy với \(x>2\)thì \(A< 0\)

ĐK \(a\ne\left\{-1;1\right\}\)
a. Ta có \(Q=\frac{a^3-3a^2+3a-1}{a^2-1}=\frac{\left(a-1\right)^3}{\left(a-1\right)\left(a+1\right)}=\frac{\left(a-1\right)^2}{a+1}\)
b. Khi \(\left|x\right|=5\Rightarrow\orbr{\begin{cases}x=5\\x=-5\end{cases}}\)
Với \(x=5\Rightarrow Q=\frac{\left(5-1\right)^2}{5+1}=\frac{16}{6}=\frac{8}{3}\)
Với \(x=-5\Rightarrow Q=\frac{\left(-5-1\right)^2}{-5+1}=\frac{36}{-9}=-4\)

Điều kiện x ≠ 2 và x ≠ 0
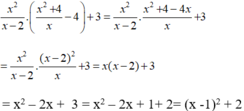
Vì x - 1 2 ≥ 0 nên x - 1 2 + 2 ≥ 2 với mọi giá trị của x.
Khi đó giá trị nhỏ nhất của biểu thức bằng 2 khi x = 1.
Vậy biểu thức đã cho có giá trị nhỏ nhất bằng 2 tại x = 1.

\(a,B=4\sqrt{x=1}-3\sqrt{x+1}+2\)\(\sqrt{x+1}+\sqrt{x+1}\)
\(=4\sqrt{x+1}\)
\(b,\)đưa về \(\sqrt{x+1}=4\Rightarrow x=15\)
a, Với \(x\ge-1\)
\(\Rightarrow B=4\sqrt{x+1}-3\sqrt{x+1}+2\sqrt{x+1}+\sqrt{x+1}\)
\(=4\sqrt{x+1}\)
b, Ta có B = 16 hay
\(4\sqrt{x+1}=16\Leftrightarrow\sqrt{x+1}=4\)bình phương 2 vế ta được
\(\Leftrightarrow x+1=16\Leftrightarrow x=15\)

Điều kiện x ≠ -2 và x ≠ 0
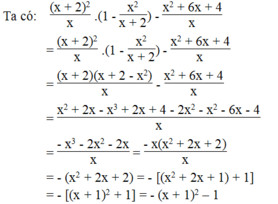
Vì x + 1 2 ≥ 0 nên - x + 1 2 ≤ 0 ⇒ - x + 1 2 - 1 ≤ - 1
Khi đó biểu thức có giá trị lớn nhất bằng -1 khi x = -1
Vậy biểu thức đã cho có giá trị lớn nhất bằng -1 tại x = -1.

a) x(x-y) + y(x+y) = x^2 - xy + yx + y^2 = x^2 + y^2 = (-6)^2 + 8^2 = 100
b) x(x^2 - y ) - x^2( x + y ) + y(x^2 - x )
= x^3 - xy - x^3 -x^2y+yx^2 - xy
= ( x^3 - x^3 ) + ( x^2 y - x^2 y ) + ( -xy - xy )
= -2xy
Bạn kiểm tra lại đề nhé!
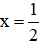 và y = –100;
và y = –100;
Bài 5:
\(A=3^{100}-3^{99}+3^{98}-3^{97}+...+3^2-3+1\\ 3A=3^{101}-3^{100}+3^{99}-3^{98}+...+3^3-3^2+3\\ 3A+A=\left(3^{101}-3^{100}+3^{99}-3^{98}+...+3^3-3^2+3\right)+\left(3^{100}-3^{99}+3^{98}-3^{97}+...+3^2-3+1\right)\\ 4A=3^{101}+1\\ A=\dfrac{3^{101}+1}{4}\)