Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a)8x3 + * + * + 27y3 = (* + *)3
=>A=(2x+3y)^3
b) (2x+1)^3
c)(x-2y)^3
d)(3x-2)(3x+2)
e)(3x-1)(9x^2+3x+1)
f)....................
6: \(27x^3+1=\left(3x+1\right)\left(9x^2-3x+1\right)\)
7: \(\left(2x+1\right)^2=4x^2+4x+1\)
8: \(\left(2x-1\right)^2=4x^2-4x+1\)
9: \(9-16x^2=\left(3-4x\right)\left(3+4x\right)\)


Câu 1:
Nhân từng hạng tử của đa thức/đơn thức này cho từng hạng tử của đa thức/đơn thức kia. Sau đó, thu gọn lại ta được kết quả cần tìm
Câu 2:
Có 7 hằng đẳng thức. Công thức:
1: \(\left(a+b\right)^2=a^2+2ab+b^2\)
2: \(\left(a-b\right)^2=a^2-2ab+b^2\)
3: \(a^2-b^2=\left(a-b\right)\left(a+b\right)\)
4: \(\left(a+b\right)^3=a^3+3a^2b+3ab^2+b^3\)
5: \(\left(a-b\right)^3=a^3-3a^2b+3ab^2-b^3\)
6: \(a^3+b^3=\left(a+b\right)\left(a^2-ab+b^2\right)\)
7: \(a^3-b^3=\left(a-b\right)\left(a^2+ab+b^2\right)\)


(a + b)^2 = a^2 + 2ab + b^2
(a - b)^2 = a^2 - 2ab + b^2
a^2 - b^2 = (a-b)(a+b)
a^3 + b^3 = (a+b)(a^2 - ab + b^2)
a^3 - b^3 = (a-b)(a^2 + ab + b^2)
Tham khảo!
1. Bình phương của một tổng
Với A, B là các biểu thức tùy ý, ta có: ( A + B )2 = A2 + 2AB + B2.
Ví dụ:
a) Tính ( a + 3 )2.
b) Viết biểu thức x2+ 4x + 4 dưới dạng bình phương của một tổng.
Hướng dẫn:
a) Ta có: ( a + 3 )2= a2+ 2.a.3 + 32 = a2 + 6a + 9.
b) Ta có x2+ 4x + 4 = x2+ 2.x.2 + 22 = ( x + 2 )2.
2. Bình phương của một hiệu
Với A, B là các biểu thức tùy ý, ta có: ( A - B )2 = A2 - 2AB + B2.
3. Hiệu hai bình phương
Với A, B là các biểu thức tùy ý, ta có: A2 - B2 = ( A - B )( A + B ).
4. Lập phương của một tổng
Với A, B là các biểu thức tùy ý, ta có: ( A + B )3 = A3 + 3A2B + 3AB2 + B3.
5. Lập phương của một hiệu.
Với A, B là các biểu thức tùy ý, ta có: ( A - B )3 = A3 - 3A2B + 3AB2 - B3.
Ví dụ :
a) Tính ( 2x - 1 )3.
b) Viết biểu thức x3- 3x2y + 3xy2- y3 dưới dạng lập phương của một hiệu.
Hướng dẫn:
a) Ta có: ( 2x - 1 )3
= ( 2x )3 - 3.( 2x )2.1 + 3( 2x ).12 - 13
= 8x3 - 12x2 + 6x - 1
b) Ta có : x3- 3x2y + 3xy2- y3
= ( x )3 - 3.x2.y + 3.x. y2 - y3
= ( x - y )3
~HT~

(a + b)n = nC0an + nC1an − 1b + nC2an − 2b2 + nC3an − 3b3 + ... + nCnbn
Đã nghĩ ra
Nhờ công thức tổ hợp và chỉnh hợp lớp 11

\(\left(\dfrac{1}{3}y+3\right)^3=\dfrac{1}{27}y^3+y^2+9y+27\)

a) Các hằng đẳng thức lượng giác cơ bản:
sin2α + cos2α = 1
1 + tan2α = 1/(cos2α); α ≠ π/2 + kπ, k ∈ Z
1 + cot2α = 1/(sin2α); α ≠ kπ, k ∈ Z
tanα.cotα = 1; α ≠ kπ/2, k ∈ Z
b) Công thức cộng:
cos(a - b) = cosa cosb + sina sinb
cos(a + b) = cosa cosb - sina sinb
sin(a - b) = sina cosb - cosa sinb
sin(a + b) = sina.cosb + cosa.sinb
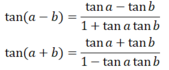
c) Công thức nhân đôi:
sin2α = 2 sinα cosα
cos2α = cos2α - sin2α = 2cos2α - 1 = 1 - 2sin2α
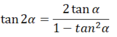
d) Công thức biến đổi tích thành tổng:
cos a cosb = 1/2 [cos(a - b) + cos(a + b) ]
sina sinb = 1/2 [cos(a - b) - cos(a + b) ]
sina cosb = 1/2 [sin(a - b) + sin(a + b) ]
Công thức biến đổi tổng thành tích:
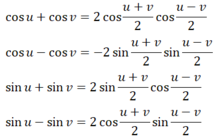
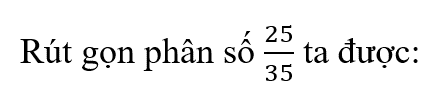
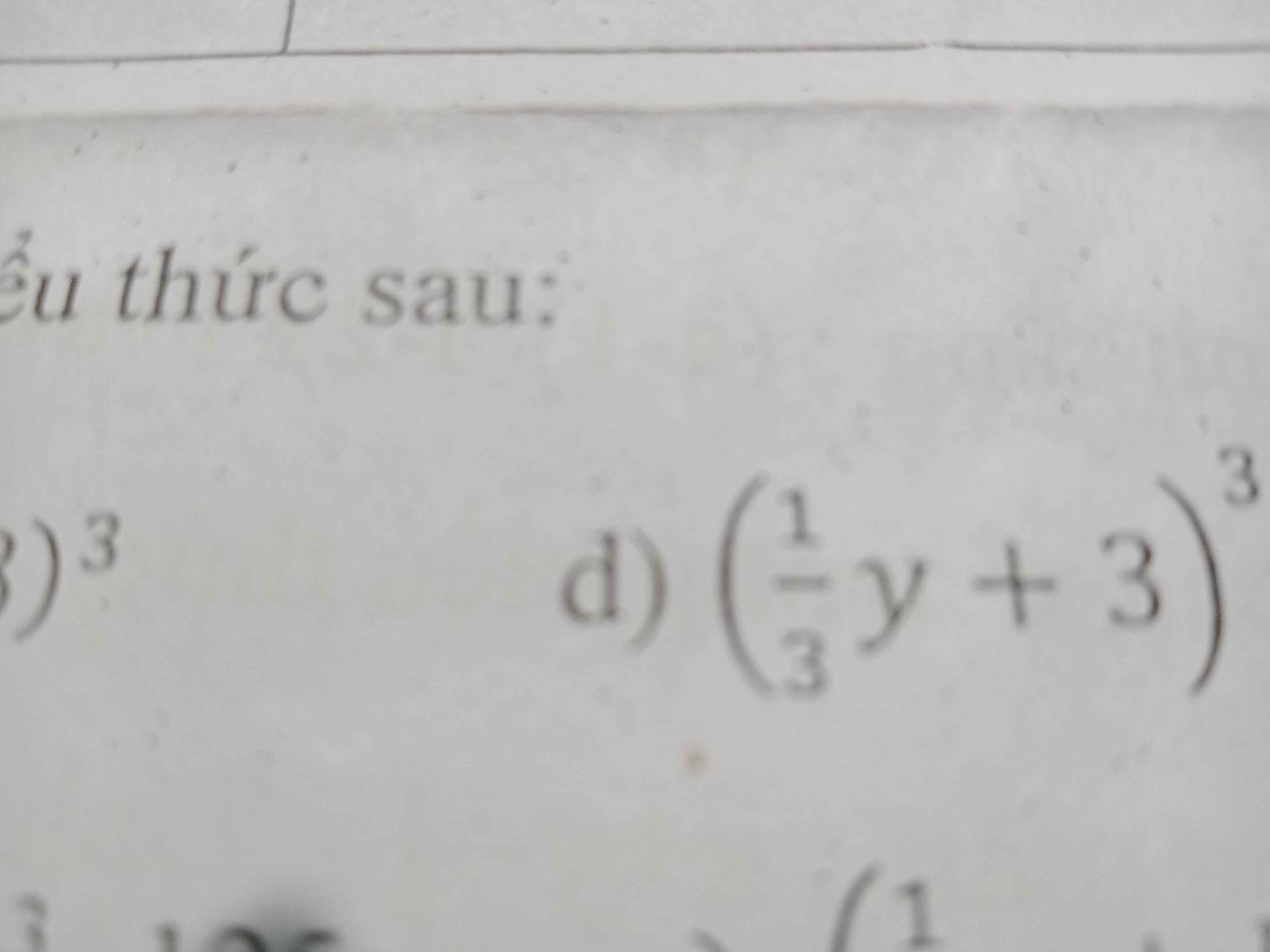
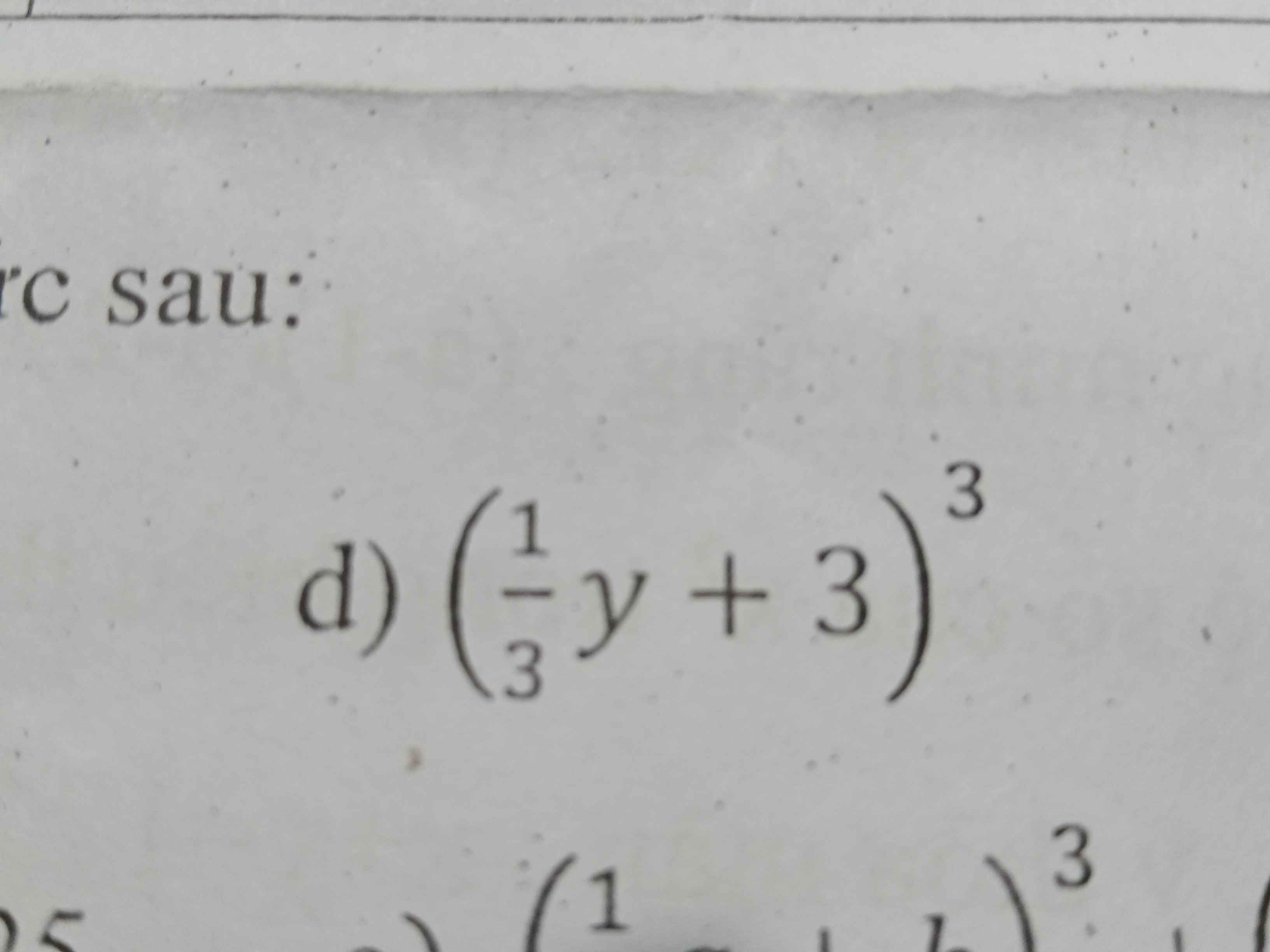
Bài 8:
\(1)\left(x+y\right)^2-\left(x-y\right)^2\\ =\left(x^2+2xy+y^2\right)-\left(x^2-2xy+y^2\right)\\ =x^2+2xy+y^2-x^2+2xy-y^2\\ =4xy\\ 2)\left(2x+3\right)^2-3x\left(2x+1\right)\\ =\left(4x^2+12x+9\right)-\left(6x^2+3x\right)\\ =4x^2+12x+9-6x^2-3x\\ =-2x^2+9x+9\\ 3)\left(4-2x\right)\left(4+2x\right)-4x\left(2x+3\right)\\ =\left[4^2-\left(2x\right)^2\right]-\left(8x^2+12x\right)\\ =16-4x^2-8x^2-12x\\ =16-12x^2-12x\\ 4)2\left(x+y\right)\left(x-y\right)+\left(x+y\right)^2-2x^2\\ =2\left(x^2-y^2\right)+\left(x^2+2xy+y^2\right)-2x^2\\ =2x^2-2y^2+x^2+2xy+y^2-2x^2\\ =x^2+2xy-y^2\)
Bài 8:
1: \(\left(x+y\right)^2-\left(x-y\right)^2\)
\(=\left(x+y+x-y\right)\left(x+y-x+y\right)\)
\(=2x\cdot2y=4xy\)
2: \(\left(2x+3\right)^2-3x\left(2x+1\right)\)
\(=4x^2+12x+9-6x^2-3x\)
\(=-2x^2+9x+9\)
3: \(\left(4-2x\right)\left(4+2x\right)-4x\left(2x+3\right)\)
\(=4^2-\left(2x\right)^2-8x^2-12x\)
\(=16-4x^2-8x^2-12x=-12x^2-12x+16\)
4: \(2\left(x+y\right)\left(x-y\right)+\left(x+y\right)^2-2x^2\)
\(=2\left(x^2-y^2\right)+x^2+2xy+y^2-2x^2\)
\(=2x^2-2y^2-x^2+2xy+y^2=x^2+2xy-y^2\)
5: \(\left(3x+4\right)\left(3x-2\right)-\left(3x+1\right)^2\)
\(=9x^2-6x+12x-8-9x^2-6x-1\)
=-9
6: \(4x\left(x-3\right)-\left(2x-1\right)\left(2x+1\right)\)
\(=4x^2-12x-\left(4x^2-1\right)\)
\(=4x^2-12x-4x^2+1=-12x+1\)
7: \(\dfrac{3}{2}x^2-\left(x-1\right)\left(x+1\right)+3x\)
\(=\dfrac{3}{2}x^2+3x-\left(x^2-1\right)\)
\(=\dfrac{3}{2}x^2+3x-x^2+1=\dfrac{1}{2}x^2+3x+1\)
8: \(2\left(5-x\right)\left(5+x\right)-\left(2x+3\right)^2-x\left(3x+2\right)\)
\(=2\left(25-x^2\right)-4x^2-12x-9-3x^2-2x\)
\(=2\left(25-x^2\right)-7x^2-14x-9\)
\(=50-2x^2-7x^2-14x-9=-9x^2-14x+41\)