Tính tổng :
A = 1/1.2 + 1/2.3 + 1/3.4 + ..............+ 1/99.100
B= 1/1.3 + 1/3.5 + 1/5.7 + ...............+ 1/97.99
Giair chi tiết .
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
25 tháng 2 2022
Câu 2:
uses crt;
var a,b:array[1..100]of integer;
i,n,t,dem,j,kt,dem1:integer;
begin
clrscr;
readln(n);
for i:=1 to n do
readln(a[i]);
t:=0;
for i:=1 to n do t:=t+a[i];
writeln(t);
dem:=1;
b[1]:=a[1];
for i:=1 to n do
begin
kt:=0;
for j:=1 to dem do
if b[j]=a[i] then kt:=1;
if kt=0 then
begin
inc(dem);
b[dem]:=a[i];
end;
end;
for i:=1 to dem do
begin
dem1:=0;
for j:=1 to n do
if a[j]=b[i] then inc(dem1);
writeln(b[i],' xuat hien ',dem1,' lan');
end;
readln;
end.
CM
29 tháng 8 2018
a) Số bị trừ của phép tính đã cho là 44- Sai vì số bị trừ là 99
b) Số trừ của phép tính đã cho là 44 - Đ
c) Tổng của hai số là 99 − 44- Sai vì 99 − 44 là một hiệu.
27 tháng 9 2016
A ) Tập hợp a là tập hợp con của b khi tất cả các phần tử có trong a phải có trong b
B ) Tập hợp a = tập hợp b khi cả hai tập hợp đều có số phần tử như nhau ! ( mình ko chắc )
c ) Phép cộng và phép nhân có những tính chất là giao hoán kết hợp , tính chất phân phối giữ phép nhân và phép cộng .
GIÚP ĐƯỢC THÌ GIÚP THÔI CHỨ MÌNH KO CHẮC !
6 tháng 10 2017
Tổng của số bị chia và số chia là
195 - 3 = 192
Tổng của số bị chia và số chia mới là
192-3=189
Số chia là
189 : (1+6)= 27
Số bị chia là
27 x 6 +3 = 165
Đ/s:số chia:27 số bị chia :165
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
14 tháng 4 2023
Tổng của hai số là:
493,2 : 2 = 246,6
Ta có sơ đồ:
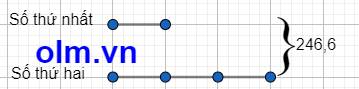
Theo sơ đồ ta có:
Số thứ nhất: 246,6 : ( 1 + 3) = 61,65
Só thứ hai: 246,6 - 61,65 = 184,95
Đáp số: a, 246,6
b, số thứ nhất 61,65
số thứ hai 184,95
8 tháng 5 2022
Ta có: 21789 : 7 = 3112 (dư 5)
Tổng của số bị chia, số chia, thương và dư của phép chia là:
21789 + 7 + 3112 + 5 = 24913
NT
Nguyễn Thành Đạt
VIP
8 tháng 5 2022
21789 :7 = 3114/dư 5
21789 + 7 = 21796 + 3114 = 24910 + 5 = 24915 HTN
\(A=\dfrac{1}{1\cdot2}+\dfrac{1}{2\cdot3}+...+\dfrac{1}{99\cdot100}\)
\(=1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{99}-\dfrac{1}{100}\)
\(=1-\dfrac{1}{100}=\dfrac{99}{100}\)
\(B=\dfrac{1}{1\cdot3}+\dfrac{1}{3\cdot5}+...+\dfrac{1}{97\cdot99}\)
\(=\dfrac{1}{2}\left(\dfrac{2}{1\cdot3}+\dfrac{2}{3\cdot5}+...+\dfrac{2}{97\cdot99}\right)\)
\(=\dfrac{1}{2}\left(1-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{5}+...+\dfrac{1}{97}-\dfrac{1}{99}\right)\)
\(=\dfrac{1}{2}\left(1-\dfrac{1}{99}\right)=\dfrac{1}{2}\cdot\dfrac{98}{99}=\dfrac{49}{99}\)