Thực hiện phép tính
\(-\dfrac{x^2}{2}+\dfrac{7}{2}x^2+x\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) Ta có: \(\dfrac{x}{x-3}-\dfrac{6}{x}-\dfrac{9}{x^2-3x}\)
\(=\dfrac{x^2}{x\left(x-3\right)}-\dfrac{6\left(x-3\right)}{x\left(x-3\right)}-\dfrac{9}{x\left(x-3\right)}\)
\(=\dfrac{x^2-6x+18-9}{x\left(x-3\right)}\)
\(=\dfrac{\left(x-3\right)^2}{x\left(x-3\right)}=\dfrac{x-3}{x}\)
b) Ta có: \(\dfrac{7}{x}-\dfrac{x}{x+6}+\dfrac{36}{x^2+6x}\)
\(=\dfrac{7\left(x+6\right)-x^2+36}{x\left(x+6\right)}\)
\(=\dfrac{7x+42-x^2+36}{x\left(x+6\right)}\)
\(=\dfrac{-\left(x^2-7x-78\right)}{x\left(x+6\right)}\)
\(=\dfrac{-\left(x^2-13x+6x-78\right)}{x\left(x+6\right)}\)
\(=\dfrac{-\left[x\left(x-13\right)+6\left(x-13\right)\right]}{x\left(x+6\right)}\)
\(=\dfrac{13-x}{x}\)
c) Ta có: \(\dfrac{6}{x-3}-\dfrac{2x-6}{x^2-9}-\dfrac{4}{x+3}\)
\(=\dfrac{6\left(x+3\right)-2x+6-4\left(x-3\right)}{\left(x-3\right)\left(x+3\right)}\)
\(=\dfrac{6x+18-2x+6-4x+12}{\left(x-3\right)\left(x+3\right)}=\dfrac{36}{\left(x-3\right)\left(x+3\right)}\)

a/ (x-1)2-(4x+3)(2-x)=x2-2x+1-(8x-4x2+6-3x)
=x2-2x+1-8x+4x2-6+3x=5x2-7x-6
b/ (15x3y2 - 6x2y3) : 3x2y2 = 5x - 2y
c/ \(\dfrac{x+7}{x-7}-\dfrac{x-7}{x+7}+\dfrac{4x^2}{x^2-49}\)=\(\dfrac{\left(x+7\right)^2-\left(x-7\right)^2+4x^2}{\left(x-7\right)\left(x+7\right)}\)=\(\dfrac{x^2+14x+49-\left(x^2-14x+49\right)+4x^2}{\left(x-7\right)\left(x+7\right)}\)=\(\dfrac{28x+4x^2}{\left(x-7\right)\left(x+7\right)}\)=\(\dfrac{4x\left(x+7\right)}{\left(x-7\right)\left(x+7\right)}\)=\(\dfrac{4x}{x-7}\)

a: Sửa đề: \(A=\dfrac{\sqrt{x}+1}{\sqrt{x}-3}\)
ĐKXĐ: \(\left\{{}\begin{matrix}x>=0\\x\ne9\end{matrix}\right.\)
Để A là số nguyên thì \(\sqrt{x}+1⋮\sqrt{x}-3\)
=>\(\sqrt{x}-3+4⋮\sqrt{x}-3\)
=>\(4⋮\sqrt{x}-3\)
=>\(\sqrt{x}-3\in\left\{1;-1;2;-2;4;-4\right\}\)
=>\(\sqrt{x}\in\left\{4;2;5;1;7;-1\right\}\)
=>\(\sqrt{x}\in\left\{4;2;5;1;7\right\}\)
=>\(x\in\left\{16;4;25;1;49\right\}\)
b: 
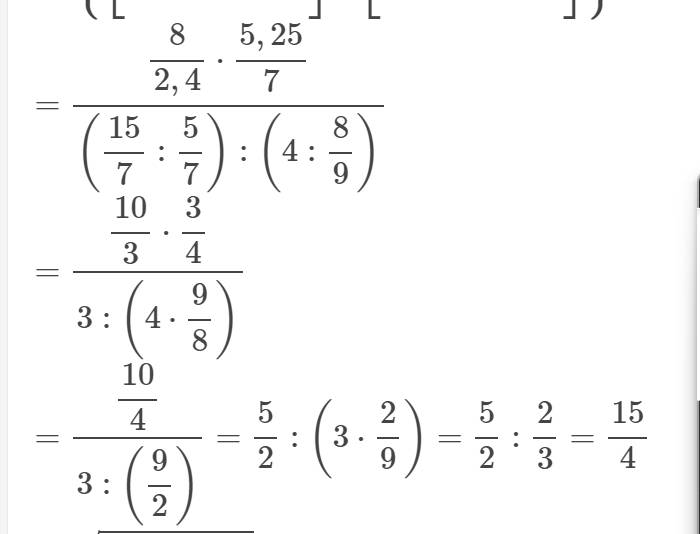

a: \(=\dfrac{7+12-6}{13}=1\)
b: \(=\dfrac{13}{10}\cdot\dfrac{6-26}{13}=\dfrac{-20}{10}=-2\)
c: \(=\dfrac{3}{4}\cdot2-\dfrac{5}{2}\cdot\dfrac{-4}{3}=\dfrac{3}{2}+\dfrac{20}{6}=\dfrac{3}{2}+\dfrac{10}{3}=\dfrac{29}{6}\)
d: \(=\dfrac{3}{8}\cdot\dfrac{8}{5}+\dfrac{3}{5}\cdot\dfrac{2}{7}+\dfrac{3}{5}\cdot\dfrac{5}{7}=\dfrac{3}{5}+\dfrac{3}{5}=\dfrac{6}{5}\)
cảm ơn bn, mình đặt câu hỏi, bn thườg xuyên trả lời câu hỏi của mình. Thank you very much.![]()

Nhận thấy \(x^3-x=x\left(x^2-1\right)=x\left(x-1\right)\left(x+1\right)\)
\(\dfrac{3}{x}-\dfrac{x}{x-1}-\dfrac{x^2}{x+1}-\dfrac{x^2-3}{x^3-x}\\ =\dfrac{3x^2-3-x^3-x^2-x^4+x^3-x^2+3}{x\left(x-1\right)\left(x+1\right)}\\ =\dfrac{-x^4+x^2}{x\left(x-1\right)\left(x+1\right)}=\dfrac{-x^2\left(x-1\right)\left(x+1\right)}{x\left(x-1\right)\left(x+1\right)}=-x\)

\(a,=\dfrac{1}{x\left(y-x\right)}-\dfrac{1}{y\left(y-x\right)}=\dfrac{x-y}{xy\left(y-x\right)}=\dfrac{-1}{xy}\\ b,=\dfrac{x+3-x-4}{x-2}=\dfrac{-1}{x-2}\)

`x/(x+y) + (2xy)/(x^2-y^2) - y(x+y)`
`= (x(x-y))/(x^2-y^2) + (2xy)/(x^2-y^2) - (y(x-y))/(x^2-y^2)`
`= (x^2 - xy + 2xy - xy + y^2)/(x^2-y^2)`
`= (x^2+y^2)/(x^2-y^2)`
\(\dfrac{x}{x+y}+\dfrac{2xy}{x^2-y^2}-\dfrac{y}{x+y}\)
\(=\dfrac{x-y}{x+y}+\dfrac{2xy}{\left(x+y\right)\left(x-y\right)}\)
\(=\dfrac{\left(x-y\right)^2}{\left(x+y\right)\left(x-y\right)}+\dfrac{2xy}{\left(x+y\right)\left(x-y\right)}\)
\(=\dfrac{x^2-2xy+y^2+2xy}{\left(x+y\right)\left(x-y\right)}\)
\(=\dfrac{x^2+y^2}{x^2-y^2}\)

Đặt \(x^2+1=a\)
Ta có: \(\dfrac{1}{x^2-x+1}-\dfrac{x^2+2}{x^2+1}+1\)
\(=\dfrac{1}{a-x}+\dfrac{a+1}{a}+1\)
\(=\dfrac{a}{a\left(a-x\right)}+\dfrac{\left(a+1\right)\left(a-x\right)}{a\left(a-x\right)}+\dfrac{a\left(a-x\right)}{a\left(a-x\right)}\)
\(=\dfrac{a+a^2-ax+a-x+a^2-ax}{a\left(a-x\right)}\)
\(=\dfrac{2a^2+2a-2ax-x}{a\left(a-x\right)}\)
\(=\dfrac{2\left(x^2+1\right)^2+2\left(x^2+1\right)-2x\left(x^2+1\right)-x}{\left(x^2+1\right)\left(x^2+1-x\right)}\)
\(=\dfrac{2\left(x^4+2x^2+1\right)+2x^2+2-2x^3-2x-x}{\left(x^2+1\right)\left(x^2-x+1\right)}\)
\(=\dfrac{2x^4+4x^2+2+2x^2+2-2x^3-3x}{\left(x^2+1\right)\left(x^2-x+1\right)}\)
\(=\dfrac{2x^4-2x^3+6x^2-3x+4}{\left(x^2+1\right)\left(x^2-x+1\right)}\)

a) \(\dfrac{2x}{x^2-6x+9}+\dfrac{x-2}{x-3}\) (ĐK: \(x\ne3\))
\(=\dfrac{2x}{\left(x-3\right)^2}+\dfrac{x-2}{x-3}\)
\(=\dfrac{2x}{\left(x-3\right)^2}+\dfrac{\left(x-2\right)\left(x-3\right)}{\left(x-3\right)^2}\)
\(=\dfrac{2x+x^2-2x-3x+6}{\left(x-3\right)^2}\)
\(=\dfrac{x^2-3x+6}{x^2-6x+9}\)
b) \(\dfrac{x^2+2}{x^3-1}+\dfrac{2}{x^2+x+1}-\dfrac{1}{x-1}\)
\(=\dfrac{x^2+2}{\left(x-1\right)\left(x^2+x+1\right)}+\dfrac{2\left(x-1\right)}{\left(x-1\right)\left(x^2+x+1\right)}-\dfrac{x^2+x+1}{\left(x-1\right)\left(x^2+x+1\right)}\)
\(=\dfrac{x^2+2+2x-2-x^2-x-1}{\left(x-1\right)\left(x^2+x+1\right)}\)
\(=\dfrac{x-1}{\left(x-1\right)\left(x^2+x+1\right)}\)
\(=\dfrac{1}{x^2+x+1}\)
\(-\dfrac{x^2}{2}+\dfrac{7}{2}x^2+x\\ =x^2\left(-\dfrac{1}{2}+\dfrac{7}{2}\right)+x\\ =3x^2+x\)
Thì bạn cứ làm thôi, đề bà đó !!!