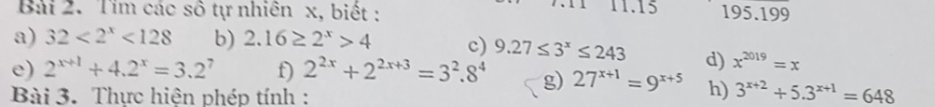
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Tổng số tự nhiên và số thập phân bằng 127,68.số thập phân có 2 chữ số.vì quên dấu phẩy ở số thập phân nên số mới gấp 100 lần số cũ tổng mới và số cũ gấp nhau số lần là:
100 - 1 = 99 (lần)
Số thập phân ban đầu là:
(5739 – 127,68):99 = 56,68
Số tự nhiên ban đầu là:
127,68 - 56,68= 71
Đáp số: Số thứ nhất: 56,68 Số thứ hai:71

Tổng hai số đó là:
2006- 4 - 31 = 1971
Số lớn là:
1971 : ( 4 + 1 ) . 4 + 31 = 1607
Số bé là:
1971 : ( 4 + 1 ) . 1 = 394,2

Giải:
Bài 1:
a) \(6^2\): 4 . 3 + 2 . \(5^2\)
= 36 : 4 . 3 + 2 . 25
= 27 + 50
= 77
77 = 7 . 11
b) 5 . \(4^2\) - 18 : \(3^2\)
= 5 . 16 - 18 : 9
= 80 - 2
= 78
78 = 2 .3 . 13
Bài 2:
a) Ta có: \(70⋮x\)
\(84⋮x\)
Do đó: \(x\inƯC\left(70;84\right)\)
\(\Leftrightarrow x\inƯ\left(14\right)\)
\(\Leftrightarrow x\in\left\{1;2;7;14\right\}\)
mà x>8
nên x=14

#include <bits/stdc++.h>
using namespace std;
long long a,b;
char st;
int main()
{
cin>>a>>b;
cout<<"Nhap phep tinh:"; cin>>st;
if (st=='+') cout<<a+b;
if (st=='-') cout<<a-b;
if (st=='*') cout<<a*b;
if (st=='/') cout<<a/b;
return 0;
}

a) 2011 : { 639 : [ 316 – ( 78 + 25 )] : 3 }
= 2011 : { 639 : [ 316 – 103 ] : 3}
= 2011 : ( 639 : 213 : 3 ) = 2011 : (3 : 3 ) = 2011 : 1 = 2011
b) ( 3x – 2 3 ) . 7 = 7 4
3x – 8 = 7 4 : 7
3x – 8 = 7 3
3x – 8 = 343
3x = 343 + 8
3x = 351
x = 351 : 3 = 117
c) (8705 + 5235) – 5x = 3885
13940 – 5x = 3885
5x = 13940 – 3885
5x = 10055
x = 10055 : 5 = 2011

Bài 2:
Ta có: \(16x+40=10\cdot3^2+5\left(1+2+3\right)\)
\(\Leftrightarrow16x+40=90+30\)
\(\Leftrightarrow16x=80\)
hay x=5
a)
\(32< 2^x< 128\\ =>2^5< 2^x< 2^7\\ =>5< x< 7\\ =>x=6\)
b)
\(2\cdot16\ge2^x>4\\ =>2\cdot2^4\ge2^x>2^2\\ =>2^5\ge2^x>2^2\\ =>5\ge x>2\\ =>x\in\left\{3;4;5\right\}\)
c)
\(9\cdot27\le3^x\le243\\ =>3^2\cdot3^3\le3^x\le3^5\\ =>3^5\le3^x\le3^5\\ =>5\le x\le5\\ =>x=5\)
d)
\(x^{2019}=x\\ =>x^{2019}-x=0\\ =>x\left(x^{2018}-1\right)=0\)
TH1: x = 0
TH2: `x^2018-1=0`
`=>x^2018=1`
`=>x^2018=1^2018`
`=>x=1` hoặc `x=-1`
a: \(32< 2^x< 128\)
=>\(2^5< 2^x< 2^7\)
=>5<x<7
mà x là số tự nhiên
nên x=6
b: \(2\cdot16>=2^x>4\)
=>\(2^5>=2^x>2^2\)
=>2<x<=5
mà x là số tự nhiên
nên \(x\in\left\{3;4;5\right\}\)
c: \(9\cdot27< =3^x< =243\)
=>\(243< =3^x< =243\)
=>\(3^x=243=3^5\)
=>x=5
d: \(x^{2019}=x\)
=>\(x\left(x^{2018}-1\right)=0\)
=>\(\left[{}\begin{matrix}x=0\\x^{2018}-1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x^{2018}=1\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=1\end{matrix}\right.\)
e: \(2^{x+1}+4\cdot2^x=3\cdot2^7\)
=>\(2^x\cdot2+4\cdot2^x=6\cdot2^6\)
=>\(6\cdot2^x=6\cdot2^6\)
=>x=6
f: \(2^{2x}+2^{2x+3}=3^2\cdot8^4\)
=>\(2^{2x}+2^{2x}\cdot8=9\cdot8^4\)
=>\(9\cdot2^{2x}=9\cdot2^{12}\)
=>2x=12
=>x=6
g: \(27^{x+1}=9^{x+5}\)
=>\(3^{3\left(x+1\right)}=3^{2\left(x+5\right)}\)
=>3(x+1)=2(x+5)
=>3x+3=2x+10
=>3x-2x=10-3
=>x=7
h: \(3^{x+2}+5\cdot3^{x+1}=648\)
=>\(3^x\cdot9+5\cdot3^x\cdot3=648\)
=>\(3^x\cdot24=648\)
=>\(3^x=\dfrac{648}{24}=27=3^3\)
=>x=3