Tim x để x2+2x-3 chia hết cho (x+1)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
29 tháng 10 2021
Bài 1:
Ta có: \(5x^3-3x^2+2x+a⋮x+1\)
\(\Leftrightarrow5x^3+5x^2-8x^2-8x+10x+10+a-10⋮x+1\)
\(\Leftrightarrow a-10=0\)
hay a=10
22 tháng 12 2021
b: \(=\dfrac{2x^4-2x^3-2x^2-3x^3+3x^2+3x+x^2-x-1}{x^2-x-1}\)
\(=2x^2-3x+1\)
27 tháng 12 2021
a: \(=\dfrac{2x^4-2x^3-2x^2-3x^3+3x^2+3x+x^2-x-1}{x^2-x-1}\)
\(=2x^2-3x+1\)
14 tháng 6 2022
Bài 13:
1: \(A=-x^2+4x+3\)
\(=-\left(x^2-4x-3\right)=-\left(x^2-4x+4-7\right)\)
\(=-\left(x-2\right)^2+7\le7\)
Dấu '=' xảy ra khi x=2
2: \(B=-\left(x^2-6x+11\right)\)
\(=-\left(x-3\right)^2-2\le-2\)
Dấu '=' xảy ra khi x=3
NV
Nguyễn Việt Lâm
Giáo viên
21 tháng 2 2020
a/ Do \(x\left(x+1\right)\) là tích 2 số nguyên liên tiếp nên chia hết cho 2
Mà 1 ko chia hết cho 2 \(\Rightarrow x\left(x+1\right)+1\) ko chia hết cho 2
b/ \(x^2+x+1=x\left(x+1\right)+1\) giống hệt câu a
c/ Do 3 chia hết cho 3 nên \(3\left(x^2+2x\right)\) chia hết cho 3
Mà 1 ko chia hết cho 3 \(\Rightarrow3\left(x^2+2x\right)+1\) ko chia hết cho 3
d/ \(3x^2+6x+1=3\left(x^2+2x\right)+1\) giống hệt câu c
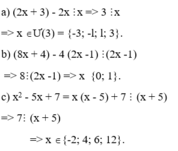
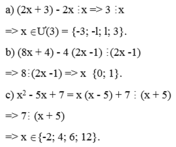
x2+2x-3 chia hết cho x+1
=> x2+x+x-3 chia hết cho x+1
Vì x2+x chia hết cho x+1
=> x-3 chia hết cho x+1
=> x+1-4 chia hết cho x+1
Vì x+1 chia hết cho x+1
=> 4 chia hết cho x+1
=> x+1 thuộc Ư(4)
KL: x\(\in\){0; -2; 1; -3; 3; -5}