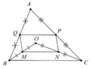
Cho tam giác ABC và một điểm M trong tam giác này. Gọi E, F, I, K theo thứ tự là trung điểm của AB, AC, MC, MB.
a) Chứng minh tứ giác KEFI là hình bình hành.
b) Xác định vị trí của điểm M để KEFI là hình chữ nhật
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1) ADME là h.b.h (vì có 2 cặp cạnh đối song song)
2) Vì ADME là hình chữ nhật nên O là trung điểm 2 đường chéo AM và DE.
Xét tam giác AHM vuông tại H, đường trung tuyến HO, khi đó HO = AO = OM
Vậy tam giác AHO cân ở O
3)
a, Tam giác ABC vuông tại A nên ˆDAE=900DAE^=900
Mà ADME là h.b.h nên tứ giác ADME là hình chữ nhật
b, Vì tứ giác AEMD là hình chữ nhật nên ED=AM
Để DE có độ dài nhỏ nhất thì AM có độ dài nhỏ nhất hay M là chân đường vuông góc hạ từ A xuống BC

a) HS tự chứng minh
b) O nằm trên đường cao xuất phát từ đỉnh A của DABC

a: Xét ΔABC có
D là trung điểm của AB
M là trung điểm của BC
Do đó: DM là đường trung bình
=>DM//AE và DM=AE
hay ADME là hình bình hành

a: Xét ΔABC có
D là tđiểm của AB
E là tđiểm của AC
Do đó: DE là đường trung bình
=>DE//FC và DE=FC
hay DECF là hình bình hành

a: Xét ΔABC có AM/AB=AN/AC
nên MN//BC và MN=BC/2
=>BC=5cm
b: Xét ΔMBC có
MK/MB=MI/MC
nên KI//BC và KI=BC/2
=>MN//KI và MN=KI
=>MNIK là hình bình hành

a: Xét ΔABC có
E là trung điểm của AB
F là trung điểm của AC
Do đó: FE là đường trung bình
=>FE//CM và FE=CM
hay FEMC là hình bình hành
a) xét tam giác ABC, có:
E là trung điểm AB (gt)
F là trung điểm AC (gt)
=> EF là đtb (đường trung bình) tam giác ABC
=> EF // BC (1)
xét tam giác BMC, có:
K là trung điểm BM (gt)
I là trung điểm MC (gt)
=> KI là đtb tam giác BMC
=> KI // BC (2)
từ (1),(2):
=> EF // KI
ta có: EF là đtb (cmt)
=>EF = \(\frac{BC}{2}\)(3)
ta có: KI là đtb (cmt)
=> KI = \(\frac{BC}{2}\)(4)
từ (3),(4):
=> EF = KI
ta có: EF // KI (cmt)
EF = KI (cmt)
=> EFIK là hbh (tứ giác có 1 cặp cạnh đối vừa = nhau vừa //)
b) chưa biết làm :V