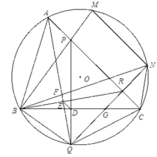
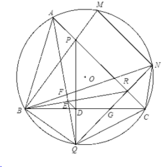
Cho tam giác ABC nội tiếp đường tròn (O), đường cao AH , trung tuyến AM. Gọi P,Q là hai điểm thuộc cung \(\widebat{BC}\)không chứa A sao cho PQ//BC và tia AP nằm giữa hai tia AQ và AB. Gọi K,L thứ tự...

B P Q ^ = B R Q ^ = R B N ^ + R N B ^ = E B F ^ + B A E ^ = 90 0 − B F E ^ + 90 0 − A B E ^ = 180 0 − B F E ^ − A B E ^ = A F B ^ − A B R ^ ⇒ A F B ^ = B P Q ^ + A B R ^

Đúng(0)

NQ

Ngô Quang Sáng

23 tháng 1 2020 - olm

1)Cho tam giác nhọn ABC (AB<AC) nội tiếp đường tròn (O). Gọi H là trực tâm của tam giác ABC, K là giao điểm thứ hai của AH với đường tròn (O). Đường thẳng đi qua H và vuông góc với OA cắt BC ở I. Chứng minh rằng IK là tiếp tuyến của đường tròn (O)2)Cho tam giác ABC (AB<AC) nội tiếp đường tròn (O), đường trung tuyến AM. Lấy điểm D trên cung BC không chứa A sao cho góc BAD= góc CAM. Chứng minh góc...

Đọc tiếp

#Toán lớp 9

6

AZ

Agatsuma Zenitsu

23 tháng 1 2020

1)Cho tam giác nhọn ABC (AB<AC) nội tiếp đường tròn (O). Gọi H là trực tâm của tam giác ABC, K là giao điểm thứ hai của AH với đường tròn (O). Đường thẳng đi qua H và vuông góc với OA cắt BC ở I. Chứng minh rằng IK là tiếp tuyến của đường tròn (O)

~~~~~~~~~ Bài làm ~~~~~~~~~

Ta có: \(\widehat{HBD}=\widehat{DAC}\) (Cùng phụ với \(\widehat{ACB}\))

\(\widehat{KBD}=\widehat{DAC}\)( Góc nối tiếp cùng chắn cung \(KC\))

\(\Rightarrow\widehat{HBD}=\widehat{KBD}\)

Ta lại có: \(BD\perp HK\)

\(\Rightarrow BD\) là đường trung trực của \(HK\)

\(\Rightarrow\Delta IHK\) cân tại \(I\)

\(\Rightarrow\widehat{BKD}=\widehat{BHD}=\widehat{AHQ}\)

Lại có:\(\widehat{DKO}=\widehat{HAO}\)( \(\Delta OKA\) cân tại \(O\))

Vì vậy: \(\widehat{DKO}+\widehat{BKD}=\widehat{HAO}+\widehat{AHQ}=90^0\)

\(\Rightarrow\widehat{KIO}=90^0\)

\(\Rightarrow IK\)là tiếp tuyến của đường tròn \(\left(O\right)\)

(Hình vẽ chỉ mang tính chất minh họa cái hình vẽ gần cả tiếng đồng hồ :)) )

Đúng(1)

NQ

Ngô Quang Sáng

24 tháng 1 2020

Ủa bạn ơi sao phụ nhau? Dòng đầu ấy

Đúng(0)

TN

tú ngọc lê

28 tháng 2 2020 - olm

Hai người cùng làm chung một công việc thì trong 4 giờ xong việc. Nếu người thứ nhất làm một mình trong 1 giờ rồi nghỉ, sau đó người thứ hai làm tiếp trong 3 giờ thì được12/5 công việc. Hỏi mỗi người làm một mình xong công việc ấy trong bao lâu?Cho tam giác ABC nhọn nội tiếp đường tròn (O), đường cao AH, đường kính AM.1. Tính góc ACM.2. Chứng minh: AB.AC = AH.AM và góc BAH = góc ACO.3. Gọi N là...

Đọc tiếp

#Toán lớp 9

0

QT

Quang Trần Minh

25 tháng 2 2018 - olm

Cho tam giác ABC vuông tại A, đường cao AH. Gọi (P), (Q) theo thứ tự là đường tròn nội tiếp hai tam giác AHB và AHC. Kẻ tiếp tuyến chung ngoài (khác BC) của hai đường tròn (P) và (Q), nó cắt AB, AH, AC theo thứ tự ở M, K, N. Chứng minh rằng:a) Các tam giác HPQ và ABC đồng dạng.b) KP // AB, KQ // AC.c) BMNC là tứ giác nội tiếp.d) Năm điểm A, M, P, Q, N thuộc cùng một đường tròn.e) Tam giác AED vuông cân (D, E...

Đọc tiếp

#Toán lớp 9

2

F

๖Fly༉Donutღღ

25 tháng 2 2018

Tự vẽ hình lấy chứ hình nó khó vẽ trên này lắm thông cảm

a) P và Q là tâm đường tròn nội tiếp các tam giác đồng dạng AHB và CHA nên

\(\frac{HP}{HQ}=\frac{AB}{AC}\)nên \(\Delta HPQ~\Delta ABC\left(c-g-c\right)\)

b) Từ câu a suy ra \(\widehat{HPQ}=\widehat{C}\)mà \(\widehat{C}=\widehat{A_1}\)

Nên \(\widehat{HPQ}=\widehat{A_1}\)( 1 )

Tứ giác HPKQ có \(\widehat{PHQ}=\widehat{PKQ}=90^o\)nên là tứ giác nội tiếp, suy ra \(\widehat{HPQ}=\widehat{HKP}\)( 2 )

Từ (1) VÀ (2) suy ra \(\widehat{A_1}=\widehat{HKP}\)do đó KP // AB. Chứng minh tương tự, KQ // AC.

c) Ta có : \(\widehat{C}=\widehat{HKP}=\widehat{MKP}\)tự chứng minh \(\widehat{MKP}=\widehat{M_1}\)(sử dụng kết quả ở câu b).

d) Ta có : \(\widehat{A_1}=\widehat{M_1}\left(=\widehat{C}\right)\)nên KM = KA. Tương tự KP =KA. Do đó năm điểm A, M, P, Q, N thuộc đường tròn (K; KA).

e) Từ câu a suy ra \(\widehat{HQP}=\widehat{C}\)nên HQEC là tứ giác nội tiếp, do đó \(\widehat{QEA}=\widehat{QHC}=45^o\)

Tam giác ADE có : \(\widehat{E}=45^o\)

\(\Rightarrow\) ADE là tam giác vuông cân.

Đúng(0)

F

๖Fly༉Donutღღ

25 tháng 2 2018

à câu cuối còn một cách nữa :)

Chứng minh \(BP\perp AQ\)tương tự ta cũng chứng minh \(CQ\perp AP\)

\(\Rightarrow\)\(AO\perp PQ\)(O là giao điểm của BP và CQ). Tam giác ADE có AO là tia phân giác góc A và \(AO\perp DE\)

\(\Rightarrow\)Tam giác AED vuông cân ( đpcm )

Đúng(0)

TA

Tran Anh

5 tháng 6 2023

Cho nửa đường tròn (O) đường kính AB, lấy hai điểm P, Q sao cho P thuộc cung AQ . Gọi C là giao điểm của tia AP và tia BQ ; H là giao điểm của AQ và BP. Chứng minh tứ giác CPHQ nội tiếp

#Toán lớp 9

1

NL

Nguyễn Lê Phước Thịnh

6 tháng 6 2023

góc APB=góc AQB=1/2*180=90 độ

=>AQ vuông góc BC, BP vuông góc CA

góc CPH+góc CQH=180 độ

=>CPHQ nội tiếp

Đúng(0)

NN

Nguyễn Ngọc Phương

22 tháng 8 2023

Cho tam giác ABC nhọn, AB > AC, đường cao BE và CF cắt nhau tại H. Gọi M là trung điểm BC. Trên tia đối của các tia AM và AC lần lượt lấy P và Q sao cho AP=AM VÀ AQ=AC.
C/m: AH vuông góc với PQ

#Toán lớp 7

1