Bài 7: Cho hình tam giác ABC có BM = MC, AD = DE = EM
a, Ghi tên tất cả các hình tam giác có chung đỉnh A và tính diện tích của từng hình tam giác đó, biết rằng diện tích tam giác BEC = 420cm2.
b, Kéo dài đoạn BE cho cắt cạnh AC ở điểm N. Hỏi M có là điểm chính giữa cạnh AC không? Vì...
Đọc tiếp
Bài 7: Cho hình tam giác ABC có BM = MC, AD = DE = EM
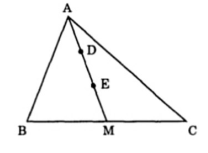
a, Ghi tên tất cả các hình tam giác có chung đỉnh A và tính diện tích của từng hình tam giác đó, biết rằng diện tích tam giác BEC = 420cm2.
b, Kéo dài đoạn BE cho cắt cạnh AC ở điểm N. Hỏi M có là điểm chính giữa cạnh AC không? Vì sao?
cái này trong đề ôn thi của mình lên thcs á
a: Vì MB=MC
nên M là trung điểm của BC
=>\(S_{EBM}=S_{EMC}=\dfrac{S_{BEC}}{2}=210\left(cm^2\right)\)
Vì AD=DE=EM
nên \(AE=\dfrac{2}{3}AM\)
Xét ΔABC có
AM là đường trung tuyến
\(AE=\dfrac{2}{3}AM\)
Do đó: E là trọng tâm của ΔABC
Các tam giác có chung đỉnh A là ΔABD,ΔABE,ΔABM;ΔACD;ΔACE;ΔACM;ΔABC
Vì AD=DE=EM
và AD+DE+EM=AM
nên \(AD=DE=EM=\dfrac{1}{3}AM\)
=>\(S_{ABD}=S_{BDE}=S_{EBM}=210\left(cm^2\right)\)
\(S_{ABE}=S_{ABD}+S_{BDE}=420\left(cm^2\right)\)
\(S_{ABM}=S_{ABD}+S_{BDE}+S_{EBM}=630\left(cm^2\right)\)
Vì AD=DE=EM
nên \(S_{ACD}=S_{DCE}=S_{EMC}=210\left(cm^2\right)\)
\(S_{AEC}=S_{ADC}+S_{DEC}=420\left(cm^2\right)\)
\(S_{AMC}=S_{ADC}+S_{DEC}+S_{EMC}=630\left(cm^2\right)\)
\(S_{ABC}=S_{AMB}+S_{AMC}=1260\left(cm^2\right)\)
b: Xét ΔABC có
E là trọng tâm
BE cắt AC tại N
Do đó: N là trung điểm của AC(ĐPCM)