Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

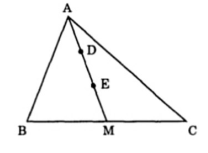
Bài 11: Cho hình vẽ bên có BM = MC. So sánh diện tích tam giác ABM với diện tích tam giác ABC.
Chọn đáp án đúng:
A. Diện tích tam giác ABM bằng một nửa diện tích tam giác ABC.
B. Diện tích tam giác ABM bằng một phần ba diện tích tam giác ABC.
C. Diện tích tam giác ABM bằng một phần tư diện tích tam giác ABC.


vô lí vì khi cắt thì bao giờ diện tích còn lại luôn nhỏ hơn diện tích ban đầu.

Bài giải:
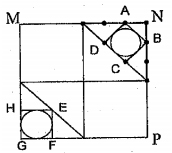
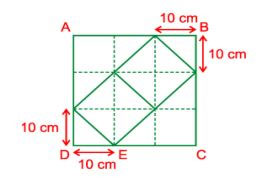
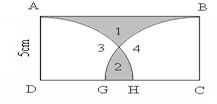
Theo đầu bài thì hình vuông ABCD được ghép bởi 2 hình vuông nhỏ và 4 tam giác (trong đó có 2 tam giác to, 2 tam giác con).
Ta thấy có thể ghép 4 tam giác con để được tam giác to đồng thời cũng ghép 4 tam giác con để được 1 hình vuông nhỏ.
Vậy diện tích của hình vuông ABCD chính là diện tích của:
2 + 2 x 4 + 2 x 4 = 18 (tam giác con).
Do đó diện tích của hình vuông ABCD là:
18 x (10 x 10) / 2 = 900 (cm2)

Theo đầu bài thì hình vuông ABCD được ghép bởi 2 hình vuông nhỏ và 4 tam giác (trong đó có 2 tam giác to, 2 tam giác con).
Ta thấy có thể ghép 4 tam giác con để được tam giác to đồng thời cũng ghép 4 tam giác con để được 1 hình vuông nhỏ.
Vậy diện tích của hình vuông ABCD chính là diện tích của 2 + 2 x 4 + 2 x 4 = 18 (tam giác con).
Do đó diện tích của hình vuông ABCD là :
\(18\times\frac{10\times10}{2}=900\left(cm^2\right)\)
Theo đầu bài thì hình vuông ABCD được ghép bởi 2 hình vuông nhỏ và 4 tam giác (trong đó có 2 tam giác to, 2 tam giác con).
Ta thấy có thể ghép 4 tam giác con để được tam giác to đồng thời cũng ghép 4 tam giác con để được 1 hình vuông nhỏ.
Vậy diện tích của hình vuông ABCD chính là diện tích của 2 + 2 x 4 + 2 x 4 = 18 (tam giác con).
Do đó diện tích của hình vuông ABCD là:
18 x (10 x 10) : 2 = 900 (cm2)
Đáp số : ............

Ta có \(\frac{BM}{BC}=\frac{1}{2}\)
Hai tg ABM và tg ABC có chung đường cao từ A->BC nên
\(\frac{S_{ABM}}{S_{ABC}}=\frac{BM}{BC}=\frac{1}{2}\Rightarrow S_{ABM}=\frac{S_{ABC}}{2}=\frac{120}{2}=60cm^2\)
b/
\(S_{ABC}=\frac{BCxAH}{2}\Rightarrow BC=\frac{2xS_{ABC}}{AH}=\frac{2x120}{15}=16cm\)
Ta có \(\frac{BM}{BC}=\frac{1}{2}\Rightarrow BM=\frac{BC}{2}=\frac{16}{2}=8cm\)


cái này trong đề ôn thi của mình lên thcs á
a: Vì MB=MC
nên M là trung điểm của BC
=>\(S_{EBM}=S_{EMC}=\dfrac{S_{BEC}}{2}=210\left(cm^2\right)\)
Vì AD=DE=EM
nên \(AE=\dfrac{2}{3}AM\)
Xét ΔABC có
AM là đường trung tuyến
\(AE=\dfrac{2}{3}AM\)
Do đó: E là trọng tâm của ΔABC
Các tam giác có chung đỉnh A là ΔABD,ΔABE,ΔABM;ΔACD;ΔACE;ΔACM;ΔABC
Vì AD=DE=EM
và AD+DE+EM=AM
nên \(AD=DE=EM=\dfrac{1}{3}AM\)
=>\(S_{ABD}=S_{BDE}=S_{EBM}=210\left(cm^2\right)\)
\(S_{ABE}=S_{ABD}+S_{BDE}=420\left(cm^2\right)\)
\(S_{ABM}=S_{ABD}+S_{BDE}+S_{EBM}=630\left(cm^2\right)\)
Vì AD=DE=EM
nên \(S_{ACD}=S_{DCE}=S_{EMC}=210\left(cm^2\right)\)
\(S_{AEC}=S_{ADC}+S_{DEC}=420\left(cm^2\right)\)
\(S_{AMC}=S_{ADC}+S_{DEC}+S_{EMC}=630\left(cm^2\right)\)
\(S_{ABC}=S_{AMB}+S_{AMC}=1260\left(cm^2\right)\)
b: Xét ΔABC có
E là trọng tâm
BE cắt AC tại N
Do đó: N là trung điểm của AC(ĐPCM)