tứ giác ABCD có M,N,P,Q thứ tự là trung điểm của AB,BC,CD,DA.E nằm ngoài tứ giác.F đối xứng với E qua M.G đối xứng với F qua N H đối xứng với G qua B.CMR:E đối xứng với H qua Q.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
24 tháng 8 2019
Ta có EBFA, FAGD, GDHC đều là hình hành. Vậy BECH cũng là hình bình hành.
Vậy E đối xứng với H qua N.
CH
Cô Hoàng Huyền
Admin
VIP
23 tháng 8 2016
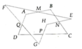
Em tự vẽ hình nhé. Ý sau cô nói rõ yêu cầu hơn là chứng minh hình bình hành MNPQ có chu vi bằng tổng độ dài hai đường chéo của tứ giác ABCD.
Xét tứ giác EFMN có OF = ON; OE = OM nên nó là hình bình hành (Tứ giác có hai đường chéo cắt nhau tại trung điểm mỗi đường)
Vậy thì MN // EF // AC và MN = EF = AC / 2 (Vì EF là đường trung bình tam giác BAC).
Hoàn toàn tương tự: QP // GH // AC và QP = GH = AC/2.
Vậy MNPQ là hình bình hành (Cặp cạnh đối song song và bằng nhau).
Khi đó ta có:
\(p_{MNPQ}=PQ+PN+NM+MQ=\left(PQ+MN\right)+\left(MQ+PN\right)=AC+BD.\)
Vậy ta đã chứng minh xong bài toán.
nhờ giải bài toán trên
nhờ giải bài toán trên