cho hình chóp SABCD có đấy ABCD là hình vuông cạnh 2a tâm O , SA vuông góc với (ABCD) và SA=3a . khoảng cách từ C đến (SBD)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\left\{{}\begin{matrix}SA\perp\left(ABCD\right)\Rightarrow SA\perp BD\\BD\perp AC\end{matrix}\right.\) \(\Rightarrow BD\perp\left(SAC\right)\)
Từ A kẻ \(AH\perp SO\Rightarrow AH\perp\left(SBD\right)\)
\(\Rightarrow AH=d\left(A;\left(SBD\right)\right)\)
\(AC=a\sqrt{2}\Rightarrow AO=\dfrac{1}{2}AC=\dfrac{a\sqrt{2}}{2}\)
Hệ thức lượng: \(\dfrac{1}{AH^2}=\dfrac{1}{SA^2}+\dfrac{1}{AO^2}\Rightarrow AH=\dfrac{SA.AO}{\sqrt{SA^2+AO^2}}=\dfrac{a\sqrt{21}}{7}\)

Đáp án là C

Ta có:
![]()
theo giao tuyến SD.
Trong (SAD) kẻ AH ⊥ DS
![]()
![]()
![]()
Ta có
![]()
Theo bài
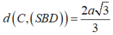

Vì tứ diện SABD có ba cạnh AS, AB, AD đôi một vuông góc nên



Do đó tam giác SAD vuông cân tại A có:
![]()


Tuy nhiên đề cho giá trị cạnh AC với BC bị sai. Cạnh huyền AC (\(a\sqrt{3}\)) sao lại có giá trị nhỏ hơn cạnh góc vuông BC (2a) nhỉ?

a: SO vuông góc (ABCD)
=>(SAC) vuông góc (ABCD)
SO vuông góc (ABCD)
=>(SBD) vuông góc (ABCD)
b: BD vuông góc AC
BD vuông góc SA
=>BD vuông góc (SAC)
d: (SB;(ABCD))=(BS;BO)=góc SBO
cos SBO=OB/SB=a*căn 2/2/(a*căn 2)=1/2
=>góc SBO=60 độ





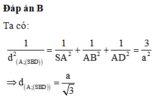
ABCD là hình vuông nên OA=OC => d( A,(SBD) ) = d( C,(SBD) )
Kẻ AH vuông SO
BD vuông AO, BD vuông SA nên BD vuông (SAO) => BD vuông AH
=> AH vuông (SBD)
=> d( A,(SBD) ) = AH
Xét SAO : \(\dfrac{1}{AH^2}\) = \(\dfrac{1}{SA^2}\) + \(\dfrac{1}{AO^2}\)
SA = 3a, AO = \(a\sqrt{2}\) => AH = \(\dfrac{3a\sqrt{22}}{11}\)
Vậy khoảng cách từ C đến (SBD) = \(\dfrac{3a\sqrt{22}}{11}\)