Một hộp đựng 15 tấm thẻ giống nhau được đánh số 1; 2;3 ; ...; 15 Bạn Lan rút ngẫu nhiên một tấm thẻ trong hộc ,Tính xác suất của các biến cố sau:
a) E: " Rút được tấm thẻ ghi số chia hết cho 3 "
b) G: " Rút được tấm thẻ ghi số nguyên tố "
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Không gian mẫu: \(C_{15}^5\)
Tổng số 5 tấm thẻ là lẻ khi số số thẻ lẻ là 1 số lẻ, gồm các trường hợp: (1 thẻ lẻ, 4 thẻ chẵn), (3 thẻ lẻ, 2 thẻ chẵn), (5 thẻ đều lẻ)
Trong 15 tấm thẻ có 7 thẻ chẵn và 8 thẻ lẻ
\(\Rightarrow\) Số biến cố thuận lợi: \(C_8^1.C_7^4+C_8^3.C_7^2+C_8^5\)
Xác suất: ...

a) Không gian mẫu là các tấm thẻ được đánh số nên nó gồm 15 phần tử, ký hiệu \(\Omega = \left\{ {1;2;3;...;15} \right\}\)
b) A là biến cố “Số ghi trên tấm thẻ nhỏ hơn 7” nên \(A = \left\{ {1;2;3;4;5;6} \right\}\)
B là biến cố “Số ghi trên tấm thẻ là số nguyên tố” nên \(B = \left\{ {2;3;5;7;11;13} \right\}\)
\(A \cup B = \left\{ {1;2;3;4;5;6;7;11;13} \right\}\)
\(AB = \left\{ {2;3;5} \right\}\)

HD: Số phần tử của không gian mẫu là: Ω = C 11 4
Gọi A là biến cố: “Tổng số ghi trên 4 tấm thẻ ấy là một số lẻ”
Khi đó số tấm lẻ được chọn là số lẻ.
Trong 11 số từ 1 đến 11 có 6 số lẻ và 5 số chẵn.


Đáp án A
Tổng cả 4 tấm thẻ là 1 số lẻ khi
+) Có 1 thẻ là lẻ, 3 thẻ còn lại là chẵn, suy ra có C 6 1 C 5 3 = 60 cách chọn.
+) Có 3 thẻ là lẻ, 1 thẻ là chẵn, suy ra có C 5 1 C 6 3 = 100 cách chọn.
Suy ra
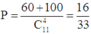

Đáp án A
Tổng cả 4 tấm thẻ là 1 số lẻ khi
+) Có 1 thẻ là lẻ, 3 thẻ còn lại là chẵn, suy ra có C 6 1 C 5 3 = 60 cách chọn.
+) Có 3 thẻ là lẻ, 1 thẻ là chẵn, suy ra có C 5 1 C 6 3 = 100 cách chọn.
Suy ra P = 60 + 100 C 11 4 = 16 33

Yêu cầu bài toán thỏa mãn khi ta rút được 3 thẻ sao cho trong đó không có 2 thẻ nào là số tự nhiên liên tiếp
Số cách rút được 3 thẻ bất kì là C 26 3
Số cách rút được 3 thẻ có đúng 2 số tự nhiên liên tiếp:
Chọn 2 số tự nhiên liên tiếp: {1;2}{2;3}…{25;26}
TH1: Chọn 2 thẻ là {1;2} hoặc{25;26}: có 2 cách
Thẻ còn lại không được là 3 (hoặc 24): 26 -3 =23 (cách)
→ 2.23 =46 (cách)
TH2: Chọn 2 thẻ là: {2;3},{3;3},…{24;25}: 23 cách
Thẻ còn lại chỉ có: 26 -4 =22 (cách) →có 23.22 =506 (cách)
Số cách rút 3 thẻ trong đó có 3 số tự nhiên liên tiếp:
{1;2;3}{2;3;4}…{24;25;26}: 24 cách
Vậy có: C 26 3 - 46 - 506 - 24 = 2024 .
Chọn đáp án D.


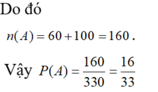


a) Có 5 tấm thẻ ghi số chia hết cho 5 có thể rút được là: \(3;6;9;12;15\)
Xác suất của biến cố E là:
\(P\left(E\right)=\dfrac{5}{15}=\dfrac{1}{3}\)
b) Có 6 tấm thẻ ghi số nguyên tố có thể rút được là: \(2;3;5;7;11;13\)
Xác suất của biến cố G là:
\(P\left(G\right)=\dfrac{6}{15}=\dfrac{2}{5}\)
a)Có 5 thuận lại cho biến cố E là: 3;6;9;12;15
Xác suất của biến cố E là:
\(\dfrac{5}{15}=\dfrac{1}{3}\)
b)Có 6 thuận lại cho biến cố E là: 2;3;5;7;11;13
Xác suất của biến cố G là:
\(\dfrac{6}{15}=\dfrac{2}{5}\)