hẹp miiiii

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đặt CTPT : \(C_xH_yO_z\)
=> \(\%m_O=100-48,65-8,11=43,24\%\)
=> \(x:y:z=\frac{48,65}{12}:\frac{8,11}{1}:\frac{43,24}{16}=4:8:3\)
=>CTPT : \(C_4H_8O_3\)

I
1. A ronot is a speacial kind of machine.
2. No, it isn't
3. Worker Robots can help make cars, and explore volcanoes, ...
4. No, it wasn't
II
1. No, there aren't. There are 2 kinds of sports.
2. Team sports require 2 separate teams.
3. Because they want to get the best score.
4. Yes, they are.

a, Nghĩa của từ động vật rộng hơn nghĩa của từ "thú", "cá" bởi vì nghĩa của từ động vật bao hàm nghĩa của từ "thú" và "cá"
b, Nghĩa của từ "thú" rộng hơn nghĩa của từ "voi", "hươu", nghĩa của từ "chim" rộng hơn nghĩa của từ "tu hú", "sáo". Nghĩa của từ "cá" rộng hơn nghĩa của từ "cá rô", "cá thu". Vì cá bao gồm nhiều loại trong đó có cá rô, cá thu.
c, Nghĩa của từ thú, cá, chim rộng hơn nghĩa của những từ voi, hươu, tu hú, sáo, cá rô, cá thu… nhưng hẹp hơn nghĩa của từ "động vật".

Phương pháp: Sử dụng công thức tính khoảng vân và điều kiện sáng tối .
Cách giải:
Ban đầu tại M là vân sáng bậc 4 , khi tăng hay giảm a một lượng thì nó trở thành vân sáng bậc k và 3k, nên ta có:
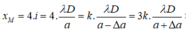
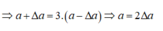
Khi tăng khoảng cách a thêm 2,5∆a thì ta có
Vậy tại M trở thành vân sáng bậc 9.
Đáp án C

D vì
Kiểu tháp ổn định (Nhật) có đặc điểm là. hẹp đáy và mở rộng hơn ở phần đỉnh
- Kiểu ổn định: tháp có dạng hẹp ở phần đáy và mở rộng hơn ở phần đỉnh; thể hiện tỉ suất sinh thấp, tỉ suất từ thấp ớ nhóm trẻ nhưng cao ở nhóm, già, tuổi thọ trung bình cao, dân số ổn định cả về quy mô và cơ cấu.

Đáp án C
Khoảng vân: ![]()
Số vân sáng, tối quan sát được trên trường giao thoa:
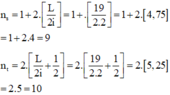
Lời giải:
PT hoành độ giao điểm của $(P)$ và $(d)$:
$x^2-(m+1)x+m-1=0(*)$
Ta thấy: $\Delta (*) = (m+1)^2-4(m-1)=m^2+2m+1-4m+4=m^2-2m+5=(m-1)^2+4>0$ với mọi $m\in\mathbb{R}$
$\Rightarrow (*)$ luôn có 2 nghiệm $x_1,x_2$ phân biệt với mọi $m$
$\Rightarrow (P)$ và $(d)$ luôn cắt nhau tại 2 điểm pb có hoành độ $x_1,x_2$ với mọi $m$
b.
Áp dụng định lý Viet:
$x_1+x_2=m+1$
$x_1x_2=m-1$
Khi đó:
$\frac{1}{y_1}+\frac{1}{y_2}=1$
$\Leftrightarrow \frac{1}{x_1^2}+\frac{1}{x_2^2}=1$
$\Leftrightarrow \frac{x_1^2+x_2^2}{x_1^2x_2^2}=1$
$\Leftrightarrow x_1^2+x_2^2=x_1^2x_2^2$
$\Leftrightarrow (x_1+x_2)^2-2x_1x_2=x_1^2x_2^2$
$\Leftrightarrow (m+1)^2-2(m-1)=(m-1)^2$
$\Leftrightarrow m^2+2m+1-2m+2=m^2-2m+1$
$\Leftrightarrow 3=-2m+1$
$\Leftrightarrow m=-1$