bể nước được làm đầu bởi vòi A và B như sau:
Nếu mở cả hai vòi A và B thì 30 phút thì đầy 1 bể.
Nếu mở vòi A trong 12 phút sau đó đóng lại và mở vòi B trong 42 phút thì đầy bể rỗng.
Hỏi cần phải mở vòi A trước B bao nhiêu phút để khi đầu bể thì lượng nước chảy ra từ 2 vòi bằng nhau?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Vì vòi A chảy 5 giờ 20 phút hay \(\frac{26}{5}h\)nên 1h vòi A chảy được \(\frac{5}{26}\)bể
Tương tự vòi B 1h chảy \(\frac{3}{13}\)bể
Tổng lượng nước chảy vào bể là: \(\frac{5}{26}+\frac{5}{26}+\frac{3}{13}=\frac{8}{13}\)(bể)
Phần bể còn lại là \(1-\frac{8}{13}=\frac{5}{13}\)(bể)
Sức chứa của bể là : \(10,4\div\frac{5}{13}=27,04\left(l\right)\)
KL:.....

- Gọi phần bể vòi thứ nhất, thứ hai chảy được trong 1 phút lần lượt là \(x,y\left(0< x,y< 1\right)\)
Đổi 1h30p=90p
- Hai vòi nước cùng chảy vào 1 bể cạn thì sau 1h30p đầy bể nên:
\(90\left(x+y\right)=1\Rightarrow x+y=\dfrac{1}{90}\left(1\right)\)
- Vòi 1 chảy trong 15p rồi đến vòi 2 chảy tiếp trong 20p được 1/5 bể nên:
\(15x+20y=\dfrac{1}{5}\left(2\right)\)
(1), (2) ta có hệ phương trình:
\(\left\{{}\begin{matrix}x+y=\dfrac{1}{90}\\15x+20y=\dfrac{1}{5}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}15x+15y=\dfrac{1}{6}\\15x+20y=\dfrac{1}{5}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x+y=\dfrac{1}{90}\\5y=\dfrac{1}{30}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{1}{225}\\y=\dfrac{1}{150}\end{matrix}\right.\)
Thời gian vòi 1 chảy để đầy bể: \(1:\dfrac{1}{225}=225\) phút = 3,75h.
Thời gian vòi 2 chảy để đầy bể: \(1:\dfrac{1}{150}=150\) phút=2,5h.
Để giải quyết bài toán này, chúng ta cần xác định lượng nước mà mỗi vòi chảy vào bể trong một giờ.
Gọi x là lượng nước mà mỗi vòi chảy vào bể trong một giờ. Theo giả thiết, khi mở cả hai vòi trong một giờ, bể sẽ được 1/3 đầy. Vì vậy, lượng nước mà mỗi vòi chảy vào bể trong một giờ là 2x (do có hai vòi).
Theo giả thiết ban đầu, nếu hai vòi cùng chảy vào bể trong 6 giờ, bể sẽ đầy. Với lượng nước mà mỗi vòi chảy vào bể trong một giờ là 2x, ta có:
6 * 2x = 1 (bể đầy)
Từ đó, ta có:
12x = 1
x = 1/12
Vậy, mỗi vòi chảy riêng thì để bể đầy, mỗi vòi sẽ mất 1/12 giờ, hay khoảng 5 phút.
Lưu ý rằng đây là một bài toán giả định, và kết quả phụ thuộc vào giả thiết ban đầu.

Gọi thời gian chảy một mình đầy bể của vòi 1 và vòi 2 lần lượt là a,b
Theo đề, ta có hệ:
1/a+1/b=1/1,5 và 1/4*1/a+1/3*1/b=1/5
=>a=15/4 và b=5/2

Gọi 1/4 số a là 0,25 . Ta có :
a . 3 - a . 0,25 = 147,07
a . (3 - 0,25) = 147,07 ( 1 số nhân 1 hiệu )
a . 2,75 = 147,07
a = 147,07 : 2,75
a = 53,48
mình nha
Bạn làm sai rồi nhưng vẫn cảm ơn bạn nha . Thầy giáo mình chữa bài này rồi . Cảm ơn Thánh Ca

đổi 3h36phut=18/5h
gọi thời gian vòi 1 mở 1 mình đầy bể là x(h)(x>18/5)
thời gian vòi 2 mở 1 mình đầy bể là y (h)(y>18/5)
vì 2 vòi cùng chảy sau 18/5h giờ đầy bể=> 1/x+1/y=5/18(1)
nếu mở vòi 1 trong 1h30=3/2h thì sau đó mới mở vòi 2 sau 3h đầy bể
=> thời gian vòi 1 chảy là 3/2+3=9/2h
thời gian vòi 2 chảy là 3h
=>9/2x+3/y=1(2)
từ (1) (2)=>hệ pt: 1/x+1/y=5/18 và 9/2x+3/y=1
đặt 1/x=a
1/y=b(a,b>0)
=>a+b=5/18 và 9a/2+3b=1
<=>a=1/9,(thỏa mãn) vafb=1/6 (thỏa mãn)
thay a=1/9 và b=1/6 vào 1/x và 1/y
=>x=9(thỏa mãn) và y=6(thỏa mãn)
vậy....
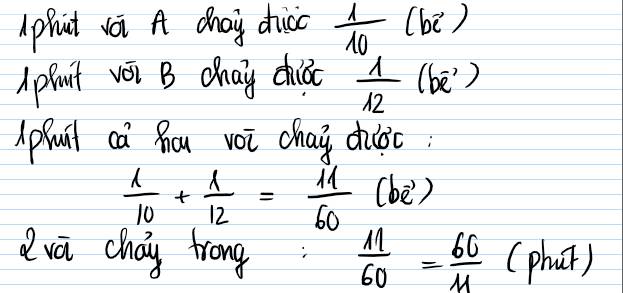
Gọi 𝐴x là lưu lượng nước của vòi A trong một phút;
y là lưu lượng nước của vòi B trong một phút.
Nếu mở cả hai vòi A và B cùng lúc, thì sau 30 phút bể đầy:
\(30\cdot\left(x+y\right)=1\left(bể\right)\)
\(\Rightarrow x+y=\dfrac{1}{30}\Rightarrow y=\dfrac{1}{30}-x\) (1)
Nếu mở vòi A trong 12 phút rồi đóng lại và mở vòi B trong 42 phút thì bể đầy: \(12x+42y=1\left(bể\right)\) (2)
Thay (1) vào (2) ta được:
\(12x+42\left(\dfrac{1}{30}-x\right)=1\)
\(\Rightarrow12x+42\cdot\dfrac{1}{30}-42x=1\)
\(\Rightarrow12x+1.4-42x=1\)
\(\Rightarrow-20x+4=1\)
\(\Rightarrow-30x=-0,4\)
\(\Rightarrow x=\dfrac{0,4}{30}=\dfrac{2}{150}=\dfrac{1}{75}\)
Thay giá trị của x vào phương trình ta được
\(\Rightarrow y=\dfrac{1}{30}-\dfrac{1}{75}=\dfrac{1}{50}\)
Vậy trong 1 phút bể A chảy được 1/75 bể và vòi chảy được 1/50 bể.
Gọi 𝑡t là thời gian mở vòi A trước khi mở vòi B. Để khi bể đầy, lượng nước chảy ra từ hai vòi bằng nhau:
\(t\cdot x=\left(30-t\right)\cdot y\)
\(\dfrac{1}{75}\cdot t=\left(30-t\right)\cdot\dfrac{1}{50}\)
\(\Rightarrow50t=75\left(30-t\right)\)
\(\Rightarrow50t=2250-75t\)
\(\Rightarrow125t=2250\)
\(\Rightarrow t=\dfrac{2250}{125}=18\)
Vậy cần mở vòi A trước 18 phút để khi bể đầy để lượng nước chảy ra từ hai vòi bằng nhau.