Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA vuông góc với đáy ABCD góc giữa hai mật phẳng (SBD) và (ABCD) bằng 60 độ. Gọi M, N lần lượt là trung điểm của SB,SC. Tính thể tích khối chóp S.ADNM
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Những câu hỏi liên quan

CM
26 tháng 10 2017
Chọn đáp án C.
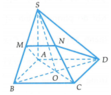
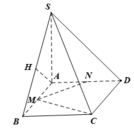
Gọi O là tâm của hình vuông ABCD thì B D ⊥ S A O



CM
1 tháng 4 2018
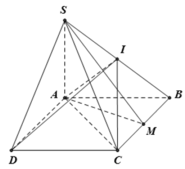
* Ta có SA ⊥ (ABCD) nên AM là hình chiếu của SM trên mặt phẳng (ABCD)
![]()
* ΔABCcó AB = BC = a ( vì ABCD là hình thoi) và ![]() nên ΔABC đều.
nên ΔABC đều.
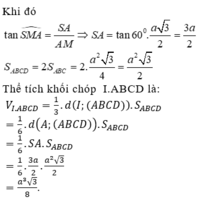

CM
12 tháng 11 2019
Chọn đáp án D
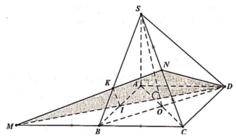
Gọi ![]()
Khi đó góc giữa 2 mặt phẳng (SBD) và (ABCD) bằng 45o![]()
Ta có: ∆BAD đều ![]()
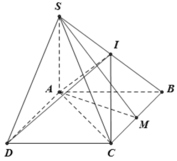
Thể tích khối chóp S.ABCD bằng: 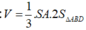
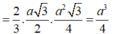
Ta có: N là trung điểm SC nên 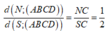
Thể tích khối chóp N.MCD bằng thể tích khối chóp N.ABCD bằng: ![]()
Ta có K là trọng tâm tam giác SMC
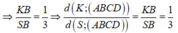
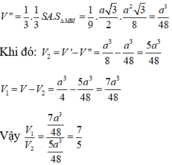
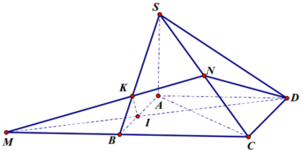
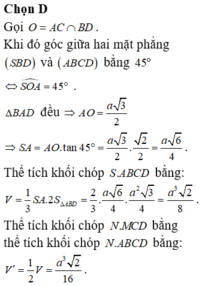
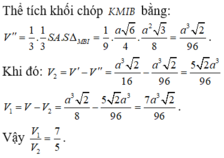






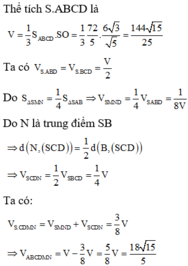


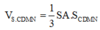
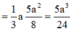
Gọi O là tâm đáy \(\Rightarrow\widehat{SOA}=60^0\)
\(\Rightarrow SA=AO.tan60^0=\dfrac{a\sqrt{6}}{2}\)
\(V_{SABC}=V_{SACD}=\dfrac{1}{2}V_{SABCD}\)
Áp dụng định lý Simsons
\(\left\{{}\begin{matrix}V_{SAMN}=\dfrac{SA}{SA}.\dfrac{SM}{SB}.\dfrac{SN}{SC}.V_{SABC}\\V_{SAND}=\dfrac{SA}{SA}.\dfrac{SN}{SC}.\dfrac{SD}{SD}.V_{SACD}\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}V_{SAMN}=\dfrac{1}{4}V_{SABC}=\dfrac{1}{8}V_{SABCD}\\V_{SAND}=\dfrac{1}{2}V_{SACD}=\dfrac{1}{4}V_{SABCD}\end{matrix}\right.\)
\(\Rightarrow V_{ADNM}=\left(\dfrac{1}{4}+\dfrac{1}{8}\right)V_{S.ABCD}\)
Định lý mới vậy anh =)) Em vừa cmt hỏi anh đoạn \(y^{\left(n\right)}\) là đạo hàm n lần đúng không ạ, chưa thấy anh phản hồi lại hóa ra anh giải giúp bài cho em.