mọi người ơi giúp mình với
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NK
1
24 tháng 4 2022
\(n_{H_2}=\dfrac{0,224}{22,4}=0,01\left(mol\right)\\
pthh:2R+2H_2O\rightarrow2ROH+H_2\)
0,02 0,01 (mol)
\(\Rightarrow M_R=0,78:0,02=39\left(\dfrac{g}{mol}\right)\)
mà R hóa trị I => R là K
8 tháng 8 2023
`@` `\text {Ans}`
`\downarrow`
Độ dài đáy của hình bình hành đó là:
`12 \times 2 = 24 (cm)`
S của hình bình hành đó là:
`12 \times 24 =288 (cm^2)`
Đáp số: `288 cm^2.`
8 tháng 8 2023
Giải :
Độ dài cạnh đáy là :
12 x 3 = 26 ( m )
Diện tích hình bình hành là :
12 x 36 = 432 ( m2 )
Đ/s :..............
mọi người ơi ai biết thì chỉ mình bài 12,13,14,15 với nha😩😩😩
25 tháng 9 2017
bài 12
điện trở tương đương của R2 và R3 là
R23=R2+R3=4+6=10(\(\Omega\))
điện trở tương đương của R4 và R5 là
R45=R4+R5=5+10=15(\(\Omega\))
điện trở tương đương của R23 và R45 là
\(\dfrac{1}{R2345}=\dfrac{1}{R23}+\dfrac{1}{R45}=\dfrac{1}{10}+\dfrac{1}{15}=\dfrac{1}{6}\)
\(\Rightarrow R2345=6\Omega\)
điện trở tương đương của R12345 là
R12345=R1+R2345=6+4=10(\(\Omega\))
điện trở tương đương của toàn mạch là
\(\dfrac{1}{Rtd}=\dfrac{1}{R12345}+\dfrac{1}{R6}=\dfrac{1}{10}+\dfrac{1}{10}=\dfrac{1}{5}\)
\(\Rightarrow Rtd=5\Omega\)
NHỚ TICK CHO MÌNH NHA CẢM ƠN
25 tháng 9 2017
BÀI 13
gọi số điện trở của 2\(\Omega\)là x(x không âm và nguyên)
gọi số điện trở của 5\(\Omega\)là y(y không âm và nguyên)
ta có 2x+5y=30(vì đây là mạch nối tiếp)
\(\Rightarrow\)2x=30-5y
\(\Rightarrow\)x=15-\(\dfrac{5y}{2}\)
đặt y=2a\(\Rightarrow\)x=15-5a
vì x,y lớn hơn 0 và sộ nguyên nên
y=2a\(\ge\)0\(\Rightarrow\)a\(\ge\)0
x=15-5a\(\ge0\Rightarrow a\le3\)
\(\Rightarrow0\le a\le3\)
\(\Rightarrow a\in0,1,2,3\)
a 0 1 2 3
x 15 10 5 0
y 0 2 4 6 (kẻ bảng nha bạn)
vậy mắc 10 điện trở 2om và 2 điện trở 5om hoặc 5 điện trở 2om và 4 điện trở 5om thì mạch mắc nối tiếp có điên trở tương đương là 30om
nhớ tick cho mk nha cảm ơn
SM
3
SM
1
SM
4
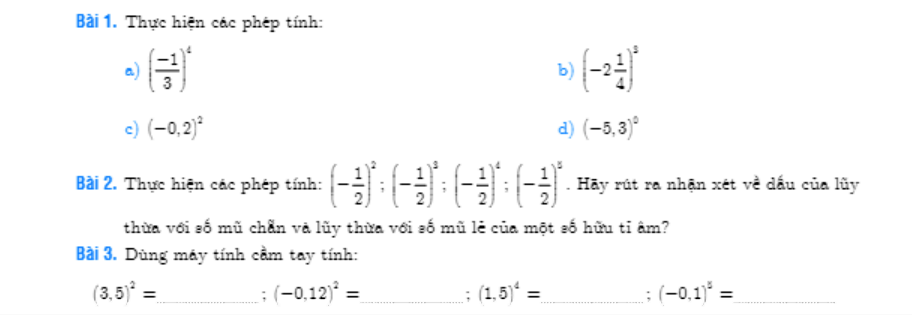
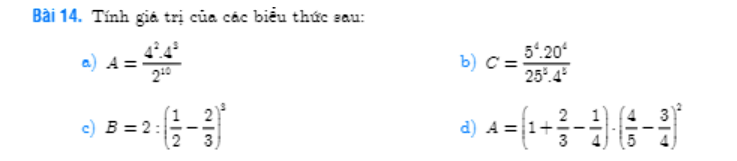
\(x^2-2mx+4m-3=0\) (1)
Ta có \(\Delta'=\left(-1\right)^2-\left(4m-3\right)=1-4m+3=-4m+4\)
Phương trình (1) có 2 nghiệm phân biệt => \(\Delta'>0\Leftrightarrow-4m+4>0\)
\(\Leftrightarrow4>4m\\ \Leftrightarrow1>m\)
Vậy phương trình có 2 nghiệm phân biệt khi m < 1
\(x^2\) - 2m\(x\) + 4m - 3 = 0
\(\Delta^,\) = 11 - (4m - 3) = 1 - 4m + 3 = 4 - 4m
Phương trình đã cho có hai nghiệm phân biệt khi và chỉ khi
\(\Delta\), > 0 ⇒ 4 - 4m > 0 ⇒ 4m < 4 ⇒ m < 1;
Kết luận phương trình đã cho có hai nghiệm phân biệt khi và chỉ khi m < 1