Cho tam giác ABC, vẽ cung tròn (A,R=BC) và cung tròn (C,R=BA). Hai cung tròn cắt nhau ở E (E nằm khác phía với B so với đường thẳng AC). Chứng minh rằng:
a, AE // BC
b, AB // CE
GIÚP MIK VS
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
zúp mik vs ko chép mạng nhaaaaaaaaa
TT
16 tháng 11 2017
Mong các bạn giải nhanh giúp mình. Mai mình phải đi học rùi!!!!
CM
23 tháng 9 2017
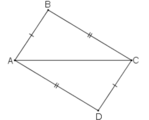
Xét ΔABC và ΔCDA, ta có:
AB = CD (theo cách vẽ)
AC cạnh chung
BC = AD (theo cách vẽ)
Suy ra: ΔABC = ΔCDA (c.c.c) ⇒ ∠(ACB) =∠(CAD) (hai góc tương ứng)
Vậy AD // BC ( vì có cặp góc so le trong bằng nhau)
TP
29 tháng 11 2021
Tham khảo
ΔΔABC và ΔΔDCB có AB=CD (gt)
BC chung AC=DB (gt)
Vậy ΔΔABC = ΔΔDCB (c.c.c)
Suy ra ˆBDC=ˆA=800BDC^=A^=800 (hai góc tương ứng)
b) Do ΔΔABC = ΔΔDCB (câu a) do đó ˆABC=ˆBCDABC^=BCD^ (hai góc tương ứng của hai tam giác bằng nhau)
Hai góc này ở vị trí so le trong của hai đường thẳng AB và CD cắt đường thẳng BC do đó CD // AB.
21 tháng 11 2015
Xét tam giác BAC và DCA có AC chung ; AB = DC vì D thuộc (C;BA) ; BC =AD ( D nằm trên (A;BC)
=> tam giác BAC =DCA (c-c-c)
=>góc BCA = góc DAC ( tương ứng) ; mà 2 góc này là SLT
= AD//BC