(m - 1)x + 1 - m2 = 0
tìm m để phương trình có nghiệm duy nhất
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(a,x=-1\\ \Leftrightarrow1-2\left(m+1\right)+m^2-3m=0\\ \Leftrightarrow-1-5m+m^2=0\\ \Leftrightarrow m^2-5m-1=0\\ \Delta=25+4=29\\ \Leftrightarrow\left[{}\begin{matrix}m=\dfrac{5+\sqrt{29}}{2}\\m=\dfrac{5-\sqrt{29}}{2}\end{matrix}\right.\)
\(b,\)Pt có 2 nghiệm phân biệt
\(\Leftrightarrow\Delta=\left[2\left(m+1\right)\right]^2-4\left(m^2-3m\right)>0\\ \Leftrightarrow4m^2+8m+4-4m^2+12m>0\\ \Leftrightarrow20m+4>0\Leftrightarrow m>-\dfrac{1}{5}\)
\(c,\)Để pt có nghiệm duy nhất (nghiệm kép)
\(\Leftrightarrow\Delta=\left[2\left(m+1\right)\right]^2-4\left(m^2-3m\right)=0\\ \Leftrightarrow20m+4=0\\ \Leftrightarrow m=-\dfrac{1}{5}\)

a: Khi m=2 thì pt sẽ là \(-x-5=0\)
hay x=-5
b: Để phương trình có nghiệm duy nhất thì m-3<>0
hay m<>3

Chọn đáp án A
Phương trình đã cho có nghiệm duy nhất khi và chỉ khi 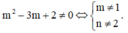

\(a,\Leftrightarrow\Delta'\ge0\\ \Leftrightarrow\left(m+2\right)^2-\left(m^2-4\right)\ge0\\ \Leftrightarrow m^2+4m+4-m^2+4\ge0\\ \Leftrightarrow4m+8\ge0\\ \Leftrightarrow m\ge-2\\ b,\Leftrightarrow\Delta'=0\Leftrightarrow m=-2\)
(m - 1)\(x\) + 1 - m2 =0
(m - 1)\(x\) = m2 - 1
Phươn trình có nghiệm duy nhất khi và chỉ khi m - 1 ≠ 0; m ≠ 1
\(x\) = \(\dfrac{m^2-1}{m-1}\)
\(x\) = m + 1
Vậy phương trình có nghiệm duy nhất \(x=m+1\) khi và chỉ khi m ≠ 1
\(\left(m-1\right)x+1-m^2=0\)
\(\Leftrightarrow\left(m-1\right)x=m^2-1\)
Pt có nghiệm duy nhất khi:
\(m-1\ne0\) \(\Rightarrow m\ne1\)