trong mặt phẳng với hệ tọa độ oxy cho tam giác abc có A(0;2) B(4;0) và trọng tâm G(7/3;1)
a, tìm tọa độ đỉnh C viết phương trình tổng quát của đường thẳng BC
b, Viết phương trình đường tròn (T) tâm A và cắt đường thẳng BC tại 2 điểm phân biệt M,N thỏa mãn MN= 2 căn 2
c, tính diện tích tứ giác...
Đọc tiếp
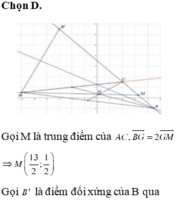
trong mặt phẳng với hệ tọa độ oxy cho tam giác abc có A(0;2) B(4;0) và trọng tâm G(7/3;1)
a, tìm tọa độ đỉnh C viết phương trình tổng quát của đường thẳng BC
b, Viết phương trình đường tròn (T) tâm A và cắt đường thẳng BC tại 2 điểm phân biệt M,N thỏa mãn MN= 2 căn 2
c, tính diện tích tứ giác AOBC
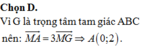
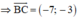
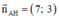là VTPT là:
a: G là trọng tâm của ΔABC
=>\(\left\{{}\begin{matrix}x_A+x_B+x_C=3\cdot x_G\\y_A+y_B+y_C=3\cdot y_G\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x_C+0+4=3\cdot\dfrac{7}{3}=7\\y_C+2+0=3\cdot1=3\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x_C=3\\y_C=1\end{matrix}\right.\)
Vậy: C(3;1)
B(4;0); C(3;1)
\(\overrightarrow{BC}=\left(-1;1\right)\)
=>Vecto pháp tuyến là (1;1)
Phương trình tổng quát của đường thẳng BC là:
1(x-4)+1(y-0)=0
=>x-4+y=0
=>x+y-4=0